Но в 1956 году голландский программист Эдсгер В. Дейкстра придумал гораздо более рациональную стратегию, позволяющую находить кратчайший маршрут между двумя городами за время, аналогичное тому, что занимает перестановка слов в алфавитном порядке. Он обдумывал практическую проблему прокладки самого быстрого маршрута между двумя голландскими городами, Роттердамом и Гронингеном.
Однажды утром мы с моей молодой невестой ходили по магазинам в Амстердаме, устали и сели на террасе кафе выпить по чашке кофе. Я размышлял, смогу ли я решить эту задачу, и вдруг разработал алгоритм кратчайшего пути. Его изобретение заняло минут двадцать… Одна из причин, по которым он получился таким изящным, в том, что я разработал его без карандаша и бумаги. Позднее я понял, что одно из преимуществ работы без карандаша и бумаги состоит в том, что это почти что вынуждает избегать всех осложнений, которых можно избежать. В конце концов, к моему огромному удивлению, этот алгоритм стал одним из краеугольных камней моей известности.
Рассмотрим следующую карту:
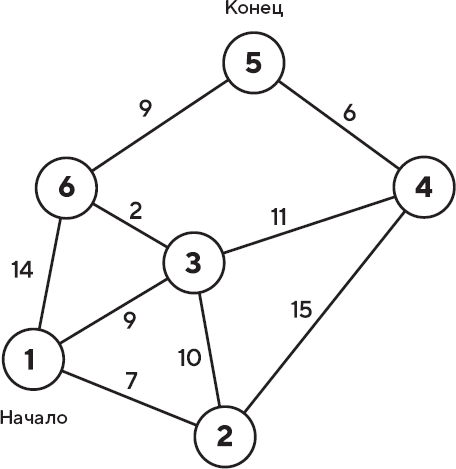
Рис. 10.3. Каков кратчайший маршрут между городами 1 и 5?
Алгоритм Дейкстры предполагает, что я начинаю путешествие из начального города, города 1. На каждом этапе я буду вычислять для каждого города промежуточную сумму расстояний, что должно помочь мне найти кратчайший маршрут. Первым делом я помечу все города, связанные с начальным, расстояниями до них. В данном случае города 2, 3 и 6 получают соответственно метки 7, 9 и 14, и первым ходом я перемещаюсь в ближайший из этих городов. Однако следует помнить, что, когда алгоритм чудесным образом решит задачу, может оказаться, что самым лучшим первым ходом был переезд совсем в другой город.
Итак, вначале я переезжаю в город 2, потому что он расположен на самом малом расстоянии от начального пункта, города 1.
Затем я присваиваю городу 1, из которого я только что уехал, метку «посещенного». Находясь в следующем пункте, городе 2, я должен изменить метки всех городов, связанных с ним. Следовательно, речь идет о городах 3 и 4. Сначала я вычисляю расстояние до них от исходного пункта, города 1, через тот пункт, в котором я нахожусь, город 2. Если новое расстояние короче, чем то, которым следующий город помечен сейчас, я присваиваю ему метку с новым расстоянием. Если новое расстояние больше, город сохраняет старую метку. В случае города 3 новое расстояние (7 + 10) больше старого; следовательно, у этого города остается старая метка с числом 9. У некоторых городов, например города 4, может не быть предыдущей метки, потому что они не связаны с городами, которые я посетил до этого. Теперь я присваиваю этим новым городам метки с только что вычисленными расстояниями до них. Таким образом, город 4 получает метку с числом 7 + 15 = 22.
Теперь я снова помечаю город, в котором я нахожусь, как посещенный и переезжаю в следующий город, имеющий самую малую текущую сумму расстояний от начального пункта. В результате описанных выше операций таким пунктом оказывается город 3. В этом примере видно, что, хотя первое перемещение в город 2 казалось рациональным, дальнейший путь из него оказывается не самым коротким. Поэтому уже на этом этапе алгоритм может склоняться к прокладке маршрута через город 3.
Оказавшись в городе 3, я снова пересчитываю метки связанных с ним городов, которые я еще не посетил. Продолжая этот процесс, я в конце концов доберусь до пункта назначения, города 5, и его метка будет обозначать кратчайшее расстояние от города, с которого я начал. Затем можно воспроизвести все перемещения в обратном порядке, чтобы выяснить, через какие города проходит маршрут, соответствующий этому расстоянию. Обратите внимание, что в описанном случае он, как выясняется, вовсе не проходит через город 2.
Какова же длительность процесса выявления кратчайшего маршрута в шагах алгоритма? При наличии
Но на практике даже то, что на этом математическом языке называется шорткатом, может требовать для получения решения чрезвычайно долгого времени. В общем случае математики действительно считают алгоритмы полиномиального времени, подобные тому, который ищем мы, шорткатами. Квадратичные алгоритмы и в самом деле работают довольно быстро. Но, хотя математики называют быстрыми и алгоритмы третьей, четвертой или пятой степени, их работа может занимать долгое физическое время.
Если компьютер способен выполнять 100 миллионов операций в секунду, это не будет слишком большой проблемой при малом
За одну секунду алгоритм сложности
Однако с практической точки зрения целесообразно бороться за алгоритмы с как можно более низкими степенями
Иголки в стогах
Вы можете надеяться, что, раз вы не коммивояжер, отсутствие шортката к прокладке кратчайшего маршрута, позволяющего объехать всех покупателей, вас не касается. Беда в том, что задач с такими же осложнениями существует очень много. Например, инженеру может понадобиться спроектировать электронную схему из сотни элементов так, чтобы робот прокладывал соединения между ними самым рациональным образом. Поскольку этот робот будет производить тысячи таких плат в сутки, сокращение времени его путешествия по соединениям этой сети даже на несколько секунд может дать компании огромную экономию средств. Но нам хотелось бы найти шорткаты не только к маршрутам перемещения по сетям. Ниже перечислены некоторые из задач, обладающих тем же качеством, что и задача коммивояжера, – задач, к решению которых, насколько нам известно, может не существовать шорткатов. Возможно, даже великий Гаусс не избежал бы при их решении долгой и нудной работы!
Задача о багажнике. Вам нужно перевезти в багажнике автомобиля коробки разных размеров. Задача требует отобрать те коробки, при укладке которых останется меньше всего неиспользованного пространства. Как выясняется, никакого рационального алгоритма, позволяющего выбрать оптимальное сочетание коробок, исходя из их размеров, не существует. Предположим, что все коробки имеют одинаковую высоту и ширину, которые точно совпадают с внутренними размерами багажника, но разную длину. Длина багажника – 150 см, а длина имеющихся в вашем распоряжении коробок равна 16, 27, 37, 42, 52, 59, 65 и 95 см. Есть ли какой-нибудь удобный способ выбрать такое сочетание коробок, которое заполнит багажник с наименьшими потерями?
Задача о расписании уроков. В начале каждого учебного года каждая школа сталкивается с задачей составления расписания для учеников. Но у возможностей распределения занятий по расписанию есть ограничения, связанные с тем, какие предметы выбирает каждый из учеников. Поскольку Ада решила заниматься химией и музыкой, уроки по этим предметам нельзя назначать на одно и то же время. А Алан выбрал химию и киноведение. Но в день может быть всего восемь уроков. Школе нужно каким-то образом втиснуть в расписание все предметы так, чтобы ни у кого не было нескольких уроков в одно и то же время. С учетом всех этих ограничений составление расписания иногда бывает похоже на укладку ковра в комнате с не вполне подходящими размерами. Не успеешь уложить ковер в одном углу, как он вспучивается в другом. Еще это похоже на решение судоку: казалось бы, все числа наконец оказались на нужных местах, как вдруг обнаруживается, что в одной из строк стоят две двойки. Черт!
Судоку. Если вы уже пытались решить какие-нибудь из самых трудных вариантов этой японской головоломки, вам случалось попадать в ситуации, в которых, по-видимому, остается только выбрать следующее число наудачу, а затем разбираться с логическими следствиями из этого решения. Если это решение было неверным и приводит к противоречию, вам остается только вернуться к тому шагу, на котором вы его приняли, и попытаться пойти по другому пути.
Задача о званом ужине. Проблема, сходная с задачей о расписании уроков, возникает, когда вы хотите пригласить друзей на ужин, но некоторые из них не ладят друг с другом, и вы не хотите приглашать их на один и тот же ужин. Чтобы определить минимальное количество ужинов, на которых у вас побывают все, но так, чтобы ни на одном из них не встретились те, кто не хочет встречаться, необходимо перебрать все возможные комбинации приглашенных.