а дороге из B в C – нить

Восемь последних оснований первой из этих дорог могут соединиться с восемью первыми основаниями второй, что показывает, что маршрут, позволяющий попасть из города А в город C, существует.

Эта система прекрасна тем, что такие нити ДНК можно приобретать в больших количествах в коммерческих лабораториях. Адлеман заказал достаточное количество материала для исследования сети из 7 городов, а затем просто разложил нити по пробиркам. Нити принялись за параллельную обработку информации: они начали соединяться, создавая множество разных маршрутов обхода сети. Разумеется, многие из этих маршрутов нарушали правило, запрещающее посещать города больше одного раза. Но Адлеман понимал, что тот маршрут, который он ищет, должен представлять собой нить ДНК, длина которой равна

Для отбора таких нитей и проверки присутствия в их последовательностях всех городов годилась процедура, сходная с генетической дактилоскопией.

Хотя весь этот процесс занял больше недели, он открыл интересные перспективы: возможность использования биологических структур для создания машин, способных эффективно производить параллельную обработку информации. Для измерения количества молекул в пробирке химики используют единицу под названием «моль». Но один моль вещества содержит чуть более 6 × 10²³ молекул[134]. Адлеман считает, что использование предельно малых биологических объектов может стать шорткатом к решению предельно больших вычислительных задач.

Не исключено, что природа уже преуспела в этом. Оказывается, один странный организм, относящийся к классу собственно слизевики, довольно хорошо умеет находить самые рациональные маршруты передвижения по карте. Это слизевик Physarum polycephalum, который представляет собой плазмодиевый одноклеточный организм, растущий вовне из исходной точки в поисках источников пищи. Его любимая еда – овсяные хлопья.

Группа исследователей из Оксфорда и Саппоро решила задать своему слизевику следующую задачу: найти кратчайший маршрут среди овсяных хлопьев, разложенных так же, как расположены станции железнодорожной сети Токио и его окрестностей. У инженеров ушли целые годы на разработку наиболее рациональной схемы соединения городов. А на что способен слизевик?

Изначально слизевик ничего не знает о местах расположения хлопьев и начинает расти во всех направлениях. Но, когда он начинает натыкаться на источники пищи, многочисленные отростки, которые пищи не нашли, отмирают, и остаются только наиболее удобные соединения с источниками пищи. Всего за несколько часов слизевик настраивает свою структуру, создавая между новыми источниками пищи соединения, удобные для достижения разных точек.

Экспериментаторов поразил тот факт, что получившаяся структура слизевика была очень похожа на схему железнодорожных сообщений, созданных людьми в окрестностях Токио. У людей на это ушли многие годы. Слизевик справился за несколько часов. Неужели это одноклеточное существо знает шорткат, который сможет помочь нам решить одну из величайших нерешенных задач математики?

Решение: На рисунке показан кратчайший маршрут по карте фестиваля Гластонбери. Чтобы убедиться, что еще более короткого маршрута не существует, мне потребовалось много времени.

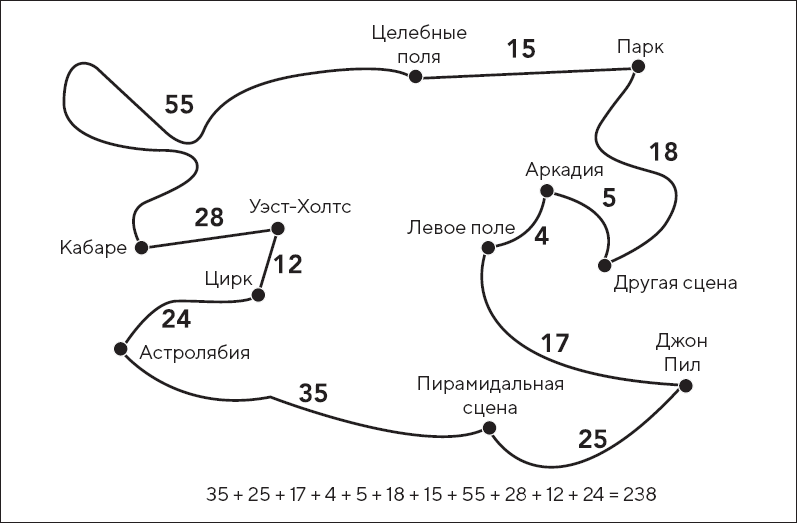
Рис. 10.5. Кратчайший маршрут обхода фестиваля Гластонбери

Шорткат к шорткатам

Иногда бывает очень важно знать, что к решению задачи, над которой вы работаете, нет никаких шорткатов. Понимание, что долгий окольный путь – это единственный путь к цели, позволяет не тратить времени на безрезультатные поиски шорткатов. А если уж вы собираетесь проделать всю необходимую работу, имеет смысл знать, что вы не напрасно тратите на нее время. Можно использовать шорткат преобразования одной задачи в другую, совершенно не похожую на первую, чтобы проверить, не пытаетесь ли вы решить, скажем, замаскированную задачу коммивояжера. Если же шорткатов действительно нет, может быть, это обстоятельство тоже можно выгодно использовать, как это делают шифровальщики.

Прибытие

Человеческая изобретательность помогла нам выдумать поразительно разнообразные шорткаты, которые на протяжении многих поколений ускоряют развитие нашего вида. Мы никогда не оказались бы в том технологически развитом состоянии, в котором мы сейчас находимся, без этого инструментария усовершенствованных способов мышления. Если нет шортката символов, обозначающих числа, все, что больше трех, называется «много». Понимание геометрии планеты упрощает физические путешествия по ней. Хотя всего 566 человек побывали в космосе[135] и никто из них не забирался дальше Луны, шорткат тригонометрии позволяет нам ориентироваться в глубинах космического пространства.

Мы нашли шорткат к путешествиям в будущее: распознавание паттернов и математический анализ помогают предугадывать дальнейшие события до того, как они произойдут. Шорткат вероятности дает нам возможность понять, какой из возможных исходов наиболее вероятен, не повторяя один и тот же опыт сотни раз. Вдумчивый анализ сетевых соединений позволяет пользоваться шорткатами, ведущими прямо к цели, вместо беспорядочных скитаний по всему интернету. Мы даже придумали новые числа, например квадратный корень из –1, чтобы создать зеркало, проходя через которое мы получаем шорткат к решениям задач. Путешествия в этот мнимый мир обеспечивают безопасную посадку вполне реальных самолетов.

Исходной причиной того, что я отправился в математическое путешествие, несомненно, было стремление уклониться от нудной и тяжелой работы. Возможность не заниматься бездумным трудом казалась ленивому подростку очень привлекательной. Я благодарен своему учителю математики, который не заставлял класс заниматься монотонными повторениями и вычислениями, а показал, что математика – это искусство находчивого мышления. Но оглядываясь назад, я также начал замечать, что в самой сути шорткатов содержится некий парадокс.