Квантовые шорткаты
Одна из проблем, с которыми сталкиваются обычные компьютеры, когда пытаются решить задачу, подобную нахождению простых чисел для деления большого кодового числа, состоит в том, что им приходится проводить одну проверку, прежде чем они могут перейти к следующей. (Уточню для ясности, что в последующих рассуждениях я имею в виду только точное деление, без остатка.) Хорошо бы было разделить компьютер на части так, чтобы все они одновременно проводили разные проверки. Параллельная обработка – очень действенный способ ускорения работы. Взять, к примеру, строительство дома. В состязании на скорость строительства дома, проводившемся в Лос-Анджелесе, победила бригада из 200 строителей, работавших параллельно: они закончили свой дом за четыре часа. Разумеется, некоторые задачи необходимо выполнять последовательно. При строительстве многоэтажного дома или подземного гаража следующий этаж можно добавить, только когда будет построен предыдущий. Но перебор меньших чисел с проверкой того, делится ли на них большее, прекрасно можно производить параллельно. Каждая из таких проверок никак не зависит от результатов всех остальных.
Недостаток параллельной обработки данных состоит в том, что и она ограничивается физическими возможностями. Если разбить задачу на две, время, которое занимают проверки, уменьшится в два раза, но зато увеличится вдвое количество необходимой аппаратуры. По сути дела, такой подход не помогает находить простые делители большого числа.
Но что, если такую параллельную обработку можно было производить без непременного удвоения аппаратуры? Такая идея пришла в голову математику Питеру Шору, работавшему в 1990-х годах в компании Bell Labs: он понял, что для одновременной проверки нескольких вещей можно использовать довольно необычные методы информатики. Речь шла о странной физике квантового мира. В квантовой физике частица – например, электрон – может находиться, по сути дела, одновременно в двух местах, пока не будет произведено ее наблюдение. Эти два положения могут соответствовать числам 0 и 1. Это называется состоянием квантовой суперпозиции. Его преимущество в том, что здесь не требуется удвоения аппаратуры: речь по-прежнему идет об одном-единственном электроне. Но этот электрон хранит не один элемент информации, а два. Такая единица информации имеет особое название – кубит. В отличие от обычных компьютеров, в которых каждый бит должен находиться либо во включенном, либо в выключенном состоянии, то есть содержать либо 0, либо 1, кубит одновременно существует в параллельных квантовых мирах: в одном из них его значение равно 0, а в другом – 1.
Таким образом, было бы полезно создать целую последовательность таких кубитов. Например, если удастся объединить 64 кубита в состоянии квантовой суперпозиции, такой массив сможет одновременно представлять все числа от 0 до 264 – 1. Обычному компьютеру пришлось бы последовательно перебирать все эти числа, присваивая каждому биту значения, равные 0 или 1. Но квантовый компьютер может сделать это одновременно. В результате мой обычный компьютер, как электрон, как бы существует в нескольких параллельных вселенных сразу. В каждой из них эти 64 кубита представляют разные числа.
Тут-то и начинается самое интересное. В каждом из параллельных миров такой компьютер проверяет, является ли то число, которое он представляет, делителем кодового числа. Но как сделать так, чтобы квантовый компьютер сумел выбрать именно тот мир, в котором кодовое число успешно делится на число проверяемое? Именно этот вопрос решает блестящий прием Шора, который он встроил в свой алгоритм. Как только мы производим наблюдение квантовой суперпозиции, она должна принять решение и окончательно перейти в одно или другое состояние. По сути дела, она выбирает положение 0 или положение 1. Переход в то или иное положение определяется вероятностью.
Шор сумел создать такой алгоритм, который обеспечивает, что после проверки на делимость в каждой из параллельных вселенных квантовая суперпозиция с подавляющей вероятностью переходит в состояние того мира, в котором проверенное число оказалось делителем кодового числа. Все остальные миры, в которых результат проверки оказался отрицательным, настолько похожи друг на друга, что они взаимно уничтожаются. Остается только тот мир, в котором деление прошло успешно.
Представьте себе двенадцать векторов, исходящих из центра циферблата часов и направленных на его числа. Если все они равной длины, то при сложении взаимно уничтожатся, и останется лишь точка в центре циферблата. Но что произойдет, если один из них будет вдвое длиннее остальных? При сложении получится вектор, указывающий в этом направлении. По существу, то же самое происходит и при квантовом наблюдении проверок на делимость.
Хотя Шор написал свою программу еще в 1994 году, создание реального квантового компьютера, на котором этот алгоритм смог бы работать, казалось несбыточной мечтой. Одна из проблем квантовых состояний – это так называемая декогеренция. 64 кубита начинают наблюдать друг друга, и суперпозиция исчезает еще до выполнения вычислений. Это одна из причин, по которым, возможно, не существует кот Шредингера – квантовый мысленный эксперимент, в котором кот, пока его не наблюдают, может быть одновременно живым и мертвым. Разумеется, электрон может находиться в состоянии суперпозиции, но как все атомы, составляющие кота, могут одновременно быть в состояниях, в которых кот мертв и жив? Среди большого количества атомов начнутся взаимодействия, и декогеренция приведет к коллапсу суперпозиции.
Однако в последние годы в области изоляции одновременных квантовых состояний были достигнуты поразительные успехи. В октябре 2019 года журнал Nature опубликовал статью исследователей из компании Google под названием «Обеспечение квантового превосходства при помощи программируемого сверхпроводящего процессора»[131]. Как сообщается в этой статье, ее авторам удалось использовать 53 кубита в состоянии суперпозиции, одновременно представляющие числа приблизительно до 1016. Их компьютер смог выполнить чрезвычайно специализированную задачу, на которую у обычного компьютера ушло бы 10 000 лет работы.
Хотя это очень радостная новость, задача, которая была поручена этому квантовому компьютеру, была не того же уровня, что поиск простых делителей больших чисел. Она была довольно сильно приспособлена именно под то оборудование, на котором она выполнялась. Многим показалось, что Google немного перебарщивает с шумихой вокруг «квантового превосходства». Группа, занимающаяся разработкой квантовых компьютеров в компании IBM, отозвалась об этой публикации весьма пренебрежительно и даже показала, что та задача, которой занимались исследователи из Google, может быть выполнена на обычном компьютере не за 10 000 лет, а за несколько дней. Несмотря на все это, достигнутый результат был поразительным. Тем не менее создание квантового компьютера, способного взламывать кредитные карты, по-видимому, все еще остается делом достаточно отдаленного будущего.
Биологические компьютеры
А как насчет задачи коммивояжера? Можно ли найти шорткат к ней при помощи нетрадиционных средств? Одну из задач, родственных задаче коммивояжера, исследователям удалось решить, применив компьютер очень необычного типа. В этой задаче – так называемой задаче о гамильтоновом пути – нужно проложить маршрут по сети дорог с односторонним движением, соединяющих нанесенные на карту города́.
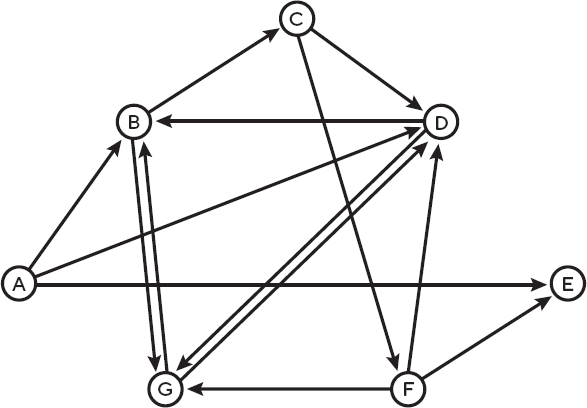
Рис. 10.4. Задача о гамильтоновом пути: как попасть из города А в город E, посетив все остальные города только по одному разу?
Требуется найти маршрут, начинающийся из одного города, скажем А, и заканчивающийся в другом городе – Е, – нопроходящий через все остальные города по одному, и только одному, разу. Возможен ли такой маршрут? Оказывается, найти его так же трудно, как решить задачу коммивояжера. Но и эта задача прекрасно подходит для применения параллельной обработки информации. Однако математик Леонард Адлеман не стал обращаться к квантовому миру, а придумал интересный биологический подход к ее решению. К слову, именно фамилию Адлемана обозначает буква А в аббревиатуре RSA, названии шифровальной системы, использующей простые числа для обеспечения безопасности сетевых транзакций.
В 1994 году Адлеман объявил на семинаре в MIT об изобретении суперкомпьютера, который он построил для решения задачи о гамильтоновом пути. Он назвал его TT-100, но его слушатели очень удивились, когда он достал из кармана пиджака обычную пробирку. Буквы ТТ означали
Нити ДНК составляются из четырех оснований, которые обозначают буквами A, T, C и G[133]. Эти основания стремятся попарно соединяться друг с другом: А с Т, а C – с G. Если получить короткие одиночные нити, составленные из этих оснований, – так называемые олигонуклеотиды, – каждая из них попытается найти другую нить, основания которой могут образовывать пары с ее собственными. Например, нить АСА попытается найти нить TGT, с которой она может соединиться и образовать устойчивую двойную нить ДНК.
Идея Адлемана состояла в следующем: присвоим каждому городу на карте, по которой мы пытаемся проложить маршрут, метку, представляющую собой нить из 8 оснований. Затем, если между двумя городами есть односторонняя дорога, создадим нить ДНК с 16 основаниями, первые 8 из которых содержатся в метке города отправления, а вторые 8 – это основания, дополнительные к содержащимся в метке города, в который ведет дорога. Если есть дорога, ведущая в город А, и дорога, ведущая из него, две нити этих дорог, содержащие по 16 оснований, соединятся: последние 8 оснований дороги, ведущей в город А, свяжутся с первыми 8 основаниями дороги, ведущей из него.
Любой маршрут проезда по этим городам по таким дорогам может быть воспроизведен в нитях ДНК, соединяющихся во всех случаях, когда одна дорога входит в город, а другая выходит из него.
Например, у города А может быть метка ATGTACCA, у города B – GGTCCACG, а у города C – TCGACCGG. Тогда дороге из А в B будет соответствовать нить