В революционной работе психологов Амоса Тверски и Даниэля Канемана были определены три основные стратегии, которые человек использует в качестве мысленных шорткатов к принятию решений. Мы используем идею паттернов, объединяющих разные события, – это явление они называют
Очевидно, две последние стратегии склонны порождать предвзятость, потому что в общем случае у нас не бывает ни очень надежных точек привязки, ни по-настоящему репрезентативных локальных знаний. В чрезвычайно влиятельной книге Канемана об ограничениях человеческой эвристики под названием «Думай медленно… решай быстро»[119] приводятся примеры того, как суждение отвечающего на вопрос можно исказить, всего лишь назвав перед этим некое число. Например, если упомянуть 1215 и 1992 годы, это искажает оценку людей, которых затем спрашивают, в каком году Альберт Эйнштейн впервые приезжал в США (правильный ответ – в 1921-м). Они называют более ранние или более поздние годы, чем респонденты, которым тот же вопрос задали без точек привязки, хотя вполне очевидно, что эти точки – то есть упомянутые годы – не имеют ни малейшего отношения к задаваемому вопросу.
Математические шорткаты, которые мы изобрели на протяжении столетий, – это попытка преодолеть действие шорткатов эволюционных, которые начинают подводить нас по мере все большего усложнения наших вопросов. Эти эвристические методы, возможно, помогали нам ориентироваться в саванне, где вероятность столкнуться с большим разнообразием предметов была меньше, но в понимании универсальных истин от них пользы мало.
Главное в полезной эвристике – понять, как понял Эйлер в случае с Кёнигсбергом, что ни характеристики мостов, ни расстояния, ни география города для задачи не существенны. Для ее решения важно лишь то, как соединены между собой участки суши.
Когда я приехал в Калининград, мне интересно было узнать, сколько из пресловутых семи мостов еще стоят в современном городе. Калининград – важный порт на Балтийском море; во время Второй мировой войны он был стратегической базой германского флота и подвергся разрушительным бомбардировкам союзной авиации. Значительная часть старого города была стерта с лица земли, в том числе и знаменитый университет, в котором изучали науки Кант и Гильберт, расположенный на острове в самом городском центре. Какова же была судьба мостов?
Три из довоенных мостов еще существуют. Два полностью исчезли. Еще два моста были разбомблены во время войны, но впоследствии заново отстроены: по ним проходит пересекающая город автострада. Однако появились два новых моста: в западной части города два берега Преголи соединяет железнодорожный мост, по которому, как я выяснил, могут ходить и пешеходы, а кроме того, был построен пешеходный Кайзеровский мост[120]. То есть мостов снова стало семь, хотя их конфигурация несколько отличается от той, которую анализировал в XVIII веке Эйлер. Разумеется, вся прелесть этого шортката состоит в том, что он действует независимо от количества и расположения мостов. Поэтому мне сразу же пришла в голову мысль проверить, можно ли проложить такой маршрут по нынешним мостам.
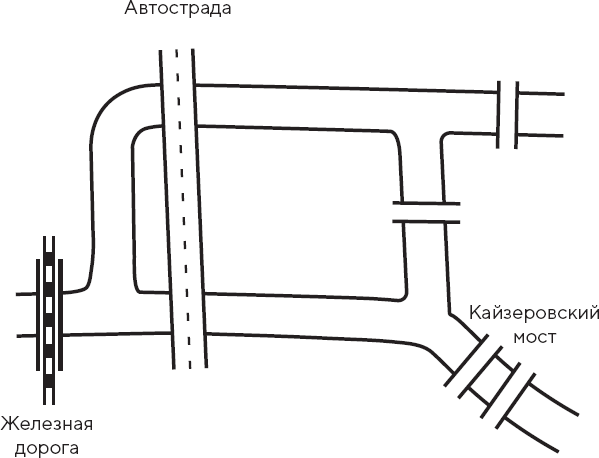
Рис. 9.4. Семь мостов в Калининграде XXI века
Как мы помним, математический анализ Эйлера показал, что маршрут всегда возможен, если есть ровно две точки, из которых ведет нечетное число мостов: нужно начать прогулку в одной из таких нечетных точек и завершить ее во второй. Если посмотреть на план мостов нынешнего Калининграда, оказывается, что такая прогулка возможна. Начав с острова в центре города, я с понятным волнением отправился в паломничество по семи калининградским мостам.
История о кёнигсбергских мостах положила начало одному из чрезвычайно важных разделов математики, играющему огромную роль в нашем мире цифровых связей, – теории сетей. А разработка шорткатов для сложных сетей, подобных интернету, принесла некоторым математикам кучу денег.
Шорткаты интернета
В интернете более 1,7 миллиарда веб-сайтов. Тем не менее, несмотря на это поразительное количество, поисковая система Google умудряется быстро находить именно ту информацию, которую вы хотите получить. Можно подумать, что это обеспечивается огромной вычислительной мощностью, и этот аспект, несомненно, тоже играет свою роль. Но по-настоящему необходимым инструментом делает Google то, как именно система ищет информацию.
В прошлом поисковые системы искали те сайты, на которых слова поискового запроса упоминаются наибольшее число раз. Если вы хотели найти подробности биографии Гаусса, поиск по словам «биография Гаусса» выдавал список сайтов, на которых эти два слова встречаются чаще всего.
Однако если бы мне захотелось распространить какие-нибудь ложные сведения о биографии Гаусса, я мог бы, вставив в метаданные своего сайта побольше слов «Гаусс» и «биография», сделать так, чтобы мой сайт с ложной информацией оказался на самом верху списка выдачи поисковых систем. Простой поиск по ключевым словам не был достаточно действенным средством для обнаружения сайтов, нужных пользователю.
Гораздо более надежное решение, позволяющее найти наилучший метод расстановки разных биографий Гаусса по значимости в списке выдачи поискового запроса, придумали два стэнфордских аспиранта, работавшие в гараже в городе Менло-Парк, – Ларри Пейдж и Сергей Брин. Они решили использовать следующую хитроумную тактику: пусть сам интернет решает, какие страницы наиболее важны. Идея состояла в том, что значимость веб-сайта можно оценить по числу ссылок на него на других веб-сайтах. На достоверную страницу с подробным изложением биографии Гаусса, вероятно, должны ссылаться другие веб-сайты, имеющие отношение к этой теме.
Но, если значение веб-сайта оценивается просто по количеству ссылок с других сайтов, у меня по-прежнему есть простой способ поднять мой лживый сайт на вершину списка выдачи. Если я сделаю тысячи фальшивых сайтов со ссылками на мою страницу с «биографией Гаусса», эта страница будет казаться наиболее значимой из всех.
У Пейджа и Брина была стратегия и против такого мошенничества. Веб-сайт сможет занять высокое положение в рейтинге, только если сайты, ссылающиеся на него, тоже занимают высокое положение. Но погодите. Кажется, тут получается порочный круг. Мне нужно знать, какие из сайтов, содержащих ссылки на мою биографию Гаусса, обладают высокой значимостью. Но и их значимость порождается ссылками на них на сайтах высокой значимости. Похоже, я попадаю в бесконечную регрессию.
Чтобы разрешить это противоречие, нужно было изначально присвоить всем веб-сайтам одинаковый статус. Пусть с самого начала у каждого веб-сайта будет десять звездочек. Но затем мы начинаем перераспределять звездочки. Если на некотором веб-сайте есть ссылки на пять других сайтов, отдадим каждому из них по две звездочки этого сайта. Если он содержит ссылки всего на два сайта, каждый из этих двух получит по пять его звездочек. Хотя исходный сайт раздает таким образом все свои звездочки, есть надежда, что он получит некоторое количество новых от других веб-сайтов, которые на него ссылаются.
Продолжая перераспределять звездочки, передавая их от одних сайтов другим, мы начинаем замечать господствующие сайты, которые собирают все больше и больше звездочек. Вскоре станет казаться (и вполне справедливо), что моя страница, на которую просто ссылается тысяча фальшивых сайтов, – всего лишь подделка. После первого же раунда передачи звездочек все сайты этой тысячи останутся без них и уже не смогут поддерживать статус моей поддельной страницы. Ее запас звездочек тоже очень быстро иссякнет, и она провалится на самый низ списка сайтов, которые оценивает алгоритм. Практическое осуществление этой идеи требует еще некоторой работы, но именно к ней сводится основной принцип ранжирования веб-сайтов в Google.
Однако для анализа перемещений звездочек по сети нужны вычислительные мощности и время. Но Брин и Пейдж поняли, что при составлении рейтингов можно воспользоваться одним шорткатом. На старших курсах университета их познакомили с одной довольно эзотерической и мудреной областью математики, в которой речь идет о так называемых «собственных значениях матриц».
Этот математический инструмент предназначен для выявления в различных динамических системах частей, остающихся неизменными. Впервые его использовал Эйлер в применении к вращающемуся шару. Если взять глобус, на поверхности которого нарисованы страны Земли, то как бы вы ни вращали и ни крутили его в руке, в его конечном положении всегда можно выбрать две противоположные точки, такие, что поворот вокруг оси, проведенной через эти точки, вернет глобус в начальное положение. По сути дела, это означает, что любое изменение ориентации глобуса может быть сведено к простому повороту вокруг некоторой оси.