Прием, который использовала Хелен, похож на то, что делал Эд Торп. Она взяла облигации в кредит и продала их по 103, но впоследствии смогла вернуть облигации изначальному владельцу, у которого она их взяла, купив их по 40, что принесло ей огромную прибыль. Она сумела извлечь выгоду из предчувствия скорого краха этих облигаций. Часто бывает нужно разглядеть истинную стоимость компании сквозь дымовую завесу ее хвастовства.
«Компании часто делятся информацией о своих проблемах не так откровенно, как следовало бы, – говорит Хелен. – Они ведут себя так же глупо, как пятидесятипятилетние мужчины, не понимающие девочек-подростков. Часто дело бывает в гордыне или в тщеславии или просто в непонимании, как устроен мир. Такого очень много в розничной торговле – с учетом всего оттока средств и дестабилизации, случившихся из-за появления интернета. Руководители многих компаний осознали, что происходит, поразительно поздно».
Мне кажется, что поиск шорткатов в некоторых областях бывает таким трудным, потому что для появления такой идеи необходимо чрезвычайно доскональное знание компании. Многое зависит от рассказов и слухов. Хелен говорит, что это похоже на просмотр мыльной оперы: «Я следила за одной испанской компанией, разрабатывавшей игры. В течение полутора лет в ней шла реструктуризация, и буквально каждый божий день мне приходилось открывать и читать аргентинские газеты, потому что бывший президент Аргентины Кристина Киршнер использовала игровую отрасль в своих политических играх. Стоимость облигаций зависела от ее заявлений!»
Хелен считает, что именно те навыки, которые она приобрела, когда получала историческое образование, дают ей шорткат к пониманию сюжета развития компаний, которые она оценивает. Когда она смотрит мыльную оперу жизни очередной компании, ей нужно угадывать, что произойдет в следующей серии, еще до ее выхода в эфир. По словам самой Хелен, ей необходимо умение сводить огромные объемы информации к чему-то полезному. Это хорошо получается именно у историков. «Это похоже на решение головоломки – точно так же, как в изучении истории. Мне нужно взять десять разных источников и сформулировать мое собственное изложение событий, какими я их вижу. Поэтому кто-нибудь другой может взять те же источники и создать совершенно другое изложение. Это необходимо для самого существования рынка. Нужно, чтобы был кто-то, кто считает, что это отличное событие, и кто-то другой, кто считает, что это конец света. Тогда и возникает торговля».
Один из ее шорткатов занимает верхнюю строчку и в моем списке математических шорткатов: умение замечать паттерны. «Паттерны можно находить в том, что случается с компаниями, и в том, что идет не так, потому что у них у всех есть одинаковые проблемы, но распределение того, что они продают, может быть несколько разным. Я стараюсь раньше других замечать паттерны в происходящем и давать рекомендации, исходя из них».
Хелен много лет занималась инвестициями в компаниях Deutsche Bank, Merrill Lynch и других, а теперь работает в компании, которая проводит по заказу инвесторов независимый анализ облигаций – как это было в случае испанской игровой компании.
Так что, если вы читаете этот пит-стоп в надежде, что я расскажу вам о каких-нибудь хитроумных шорткатах к успешным инвестициям ваших сбережений, я бы посоветовал вам угадывать содержание следующей серии мыльной оперы, которую мы называем рынком, используя таланты математиков в сочетании с глубокими знаниями специалистов, подобных Хелен с ее историческим образованием. Как говорил Ньютон, иногда лучшим шорткатом бывает возможность стоять на плечах гигантов.
9
Шорткаты сетевые
Начертите следующую фигуру, не отрывая карандаш от бумаги и не проводя ни одну из линий дважды:
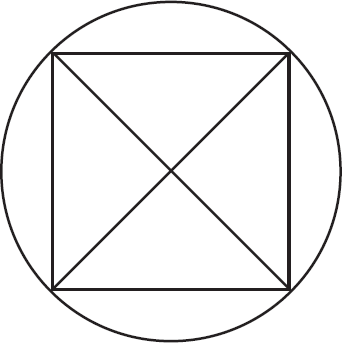
Рис. 9.1. Задача по черчению
Наш путь по современному миру все в большей степени определяется сетями. Системы автомобильных шоссе, железных дорог и маршрутов авиаперелетов позволяют нам перемещаться из одного конца планеты в другой. Находить наиболее рациональные маршруты в этой запутанной паутине помогают разнообразные программные приложения. Компании, подобные Facebook и Twitter, расширяют сферу нашего социального общения далеко за пределы деревни, в которой мы живем. Главная сеть, по которой все человечество ежедневно путешествует целыми часами, стала настоящим альтернативным миром – я говорю об интернете. Поисковая система Google добилась успеха при помощи создающего шорткаты алгоритма PageRank, помогающего пользователям ориентироваться в этой паутине, содержащей более 2 миллиардов сайтов. Хотя мы считаем интернет явлением сравнительно новым, на самом деле первые догадки о возможности сетей такого рода появились еще в XIX веке, и автором их был мой любимый мастер шорткатов.
Карл Фридрих Гаусс увлекался физикой не меньше, чем математикой. Он сотрудничал во многих проектах с одним из ведущих геттингенских физиков Вильгельмом Вебером. Гаусс даже изобрел шорткат, избавлявший от необходимости ходить между геттингенской обсерваторией и лабораторией Вебера. Он протянул между ними телеграфную линию, позволявшую переговариваться, не встречаясь лично. Эта линия длиной около трех километров проходила над городскими крышами. Гаусс и Вебер понимали, какие возможности в области связи на расстоянии открывает электромагнетизм. Они разработали код, в котором каждая буква обозначалась последовательностью положительных и отрицательных электрических импульсов. Было это в 1833 году, за несколько лет до того, как аналогичная идея пришла в голову Сэмюэлу Морзе.
Гаусс считал это изобретение своего рода любопытной безделушкой, но Вебер понимал важность таких технологий: «Когда весь земной шар будет покрыт сетью железных дорог и телеграфных проводов, эта сеть будет выполнять функции, подобные функциям нервной системы в человеческом теле, отчасти в качестве транспортного средства, а отчасти – в качестве средства молниеносного распространения идей и ощущений». Учитывая стремительное распространение телеграфа, Гаусса и Вебера можно считать прародителями интернета. Их сотрудничество увековечено в памятнике им обоим, стоящем в Геттингене.
Как и предсказывал Вебер, сегодня эта сеть охватывает гораздо большие пространства, нежели несколько километров проволоки, которые двое ученых протянули по крышам Геттингена. Более того, она стала настолько сложной, что поиск шорткатов в сетях стал одной из основных задач современной математики. Эти сети могут состоять не только из проводов, но и из мостов, как я выяснил во время недавней поездки в Россию.
Читайте Эйлера. Читайте Эйлера. Он всем нам учитель
Несколько лет назад, когда я летел в Калининград, я постарался сделать так, чтобы на короткий перелет из Санкт-Петербурга у меня было место у окна. Я совершал паломничество в город, ставший местом действия одного из рассказов, на которых воспитываются все математики, – рассказа об одном из самых изобретательных шорткатов во всей истории математики.
Подлетая к Калининграду, маленькому эксклаву Российской Федерации, отделенному от ее основной территории Литвой и Польшей, я видел реку Преголю, протекающую через город. У реки есть два рукава, сходящиеся в Калининграде; от этого места она течет дальше на запад, к месту впадения в Балтийское море. В центре города расположен остров, обтекаемый рукавами реки. В самом сердце математической истории, прославившей Калининград, как раз и находятся мосты, соединяющие берега реки друг с другом и с этим островом.
История эта относится к XVIII веку, когда у города было другое название – Кёнигсберг. Он был родиной Иммануила Канта и знаменитого математика Давида Гильберта. В то время он входил в состав Пруссии, и через Преголю были перекинуты семь мостов[117]. Одним из любимых занятий обитателей города стало следующее развлечение: по воскресеньям после обеда они пытались найти такой маршрут, который проходил бы по всем мостам, но только по одному разу. Но как бы они ни старались, всегда находился один мост, до которого они добраться не могли. В самом ли деле это было невозможно, или все же был какой-нибудь способ, позволявший перейти через все семь мостов, до которого горожане просто не додумались?
Жителям Кёнигсберга казалось, что нет никакого способа избежать утомительной ходьбы по городу, пробуя поочередно все маршруты, проходящие по мостам, пока не будут исчерпаны все возможные варианты. При этом всегда оставалось подспудное ощущение, что, возможно, какой-нибудь хитроумный путь, дающий решение этой задачи, так и остался незамеченным.