Поэтому планеты, обращающиеся вокруг Солнца, следует считать не объектами, которые притягивает сила, подобная прикрепленной к ним веревке, а просто шарами, скатывающимися по поверхности в этой четырехмерной пространственно-временной геометрии. Эта идея казалась безумной, но Эйнштейн нашел средство проверить ее на практике. Свет, как и планеты, должен находить кратчайший путь через пространство. Если свету нужно пройти вблизи массивного объекта, согласно этой теории кратчайшим путем будет обходная траектория, искривляющаяся вокруг такого объекта.
Британский астроном Артур Эддингтон понял, что эту идею можно проверить, использовав солнечное затмение, которое должно было случиться на Земле в 1919 году. Теория предсказывала, что свет от удаленных звезд должен искривляться гравитационным воздействием Солнца. Затмение было нужно Эддингтону, чтобы исчезло сияние Солнца, не позволяющее увидеть звезды. Тот факт, что свет действительно кажется огибающим объекты с большой массой, подтвердил, что кратчайшие пути – это линии не прямые, а искривленные, как и предсказывала теория Эйнштейна.
Изгибание и искривление пространства также может создавать шорткаты через Вселенную, позволяющие обойти некоторые из препятствий, существование которых предполагает теория относительности Эйнштейна. Он выяснил, что во Вселенной существует предельная скорость – скорость света в вакууме. Ничто не может двигаться быстрее. Это создает трудности для желающих переместиться с одного края галактики на другой. Такое путешествие займет много времени. Это крупная проблема, с которой сталкиваются многие писатели-фантасты: как доставить персонажей из одного места в другое, не тратя на путешествие долгие годы? Решением часто бывает использование кротовой норы, специального решения уравнений поля теории Эйнштейна, которое предполагает теоретическую возможность существования шорткатов между разными областями пространственно-временной геометрии. Кротовая нора несколько похожа на туннель, пробитый сквозь гору, но соединяет две точки в разных концах Вселенной, обычное путешествие между которыми заняло бы миллионы лет.
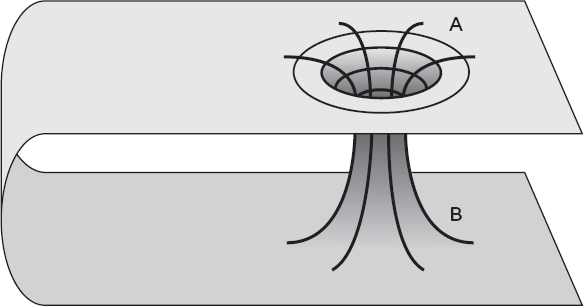
Рис. 4.7. Из точки А в точку B можно попасть длинным путем через всю Вселенную или коротким путем через кротовую нору
Таким образом, идея Гаусса о том, что свет, распространяющийся между вершинами холмов в Геттингене, использует искривленные короткие пути, была правильной. Дело было лишь в том, что увидеть этот эффект позволяют наблюдения на гораздо большем масштабе, не Ганновера, а нашей Галактики. К чести Эйнштейна, он всегда признавал, что именно математики XIX века создали геометрию, позволившую ему разработать теорию относительности: «Значение К. Ф. Гаусса для развития современной физической теории и в особенности для создания математического основания теории относительности огромно», – писал он. И еще: «Более того… я без колебаний признаю, что до некоторой степени сходное наслаждение можно получить, погрузившись в рассмотрение вопросов геометрии».
Шорткат к шорткатам
Если вы собираетесь поехать из пункта А в пункт Б, часто имеет смысл помнить, как находит самый быстрый маршрут свет: иногда бывает выгодно двигаться в обход, потому что эта дорога оказывается более быстрой, хоть и более длинной. Иногда бывает непросто измерить что-либо в доме, потому что не везде удается развернуть рулетку. Но, наверное, можно измерить углы? Синусы и косинусы всегда были предназначены открывать поразительно удобные шорткаты к измерению не только ночного неба или поверхности Земли, но всего того, что на первый взгляд может показаться недоступным. Стратегию градостроителей – предоставлять жителям самим находить шорткаты – можно использовать не только для переходов из одного конца парка в другой. Когда вы следуете за общественностью к оптимальному решению какой-либо задачи, это может стать шорткатом, который избавит вас от необходимости выполнять всю соответствующую работу самостоятельно.
Пит-стоп: Путешествия
Я очень люблю гулять. Неспешная ходьба позволяет воспринимать пейзажи и природу так, как это редко удается делать в нашей суматошной жизни. Цель прогулки – не перемещение из пункта А в пункт Б. Зачастую речь идет о перемещении из пункта А в пункт А с получением удовольствия от длинного кружного пути, заканчивающегося там же, где он начинался. Когда мой сын был маленьким, это занятие казалось ему бессмысленным. Однажды мы вышли в однодневный пеший поход по сельской местности. Через пару километров сын внезапно заметил тропу, отходившую от нашего пути и пересекавшую поле. В ее конце он увидел наш дом. «Пап, я нашел шорткат! Смотри, нам надо пойти по этой тропинке, и она приведет прямо к дому!»
Но для меня пешие прогулки – это еще и своего рода шорткат. Мне кажется, что три мили в час[60] – идеальная скорость для размышлений. Жан-Жак Руссо писал в «Исповеди»: «Ходьба таит в себе нечто такое, что оживляет и заостряет мои мысли; я почти совсем не могу думать, сидя на месте; нужно, чтобы тело мое находилось в движении, чтобы пришел в движение и ум»[61]. Прогулки – мой шорткат к математическим озарениям, необходимая кружная дорога, по которой мне нужно пройти, чтобы позволить моему подсознанию изучить задачу с новой стороны.
Роберт Макфарлейн говорит о связи между ходьбой и мышлением в книге «Старые пути» (The Old Ways: A Journey on Foot, 2012). Он описывает, как Людвиг Витгенштейн, гуляя по сельской местности в Норвегии, сделал важный шаг в своей работе. «Мне кажется, что я родил внутри себя новые мысли», – пишет философ. Но наиболее показательно, как отмечает Макфарлейн, то слово, которым Витгенштейн называет эти мысли. Витгенштейн использует слово
Макфарлейн любит путешествия, прогулки на природе, походы, поездки. Его книги – великолепная хвалебная речь пешим путешествиям. Поэтому мне очень хотелось поговорить с ним о том, как он относится к идее шорткатов. Не упускаем ли мы чего-нибудь из виду, если всегда стремимся найти шорткат?
«Я могу подняться на вершину Каирн-Горм в моих любимых горах на северо-востоке Шотландии на фуникулере и почувствовать, что это кратчайший путь до вершины, но она не принесет мне почти никакого удовлетворения или удовольствия, – говорит он. – Но, если я доберусь до той же вершины после двухдневного пешего восхождения, она будет одним из самых поразительных мест, в каких я когда-либо бывал».
Макфарлейн рассказал мне о шотландском альпинисте и мистике У. Х. Мюррее, в чьих сочинениях отразились те сильные ощущения, которые испытываешь, находясь в таких местах: «Когда дух человека испытывает угнетение или облегчение, его сердце естественным образом стремится вверх». Мюррей писал эти слова на туалетной бумаге, которую он копил, находясь в заключении – в лагере для военнопленных во время Второй мировой войны[62]. Хотя его тело не имело возможности путешествовать, его разум странствовал по Шотландскому высокогорью. Другим героем Макфарлейна стала модернистская писательница и поэтесса Нэн Шеперд.
«В сороковых годах Нэн Шеперд писала в конце “Живой горы”[63], что эти, как она их называет вслед за Вулф и Вордсвортом и другими, моменты бытия возникают, только когда “мы бродим так, с обостренными чувствами, час за часом, пока наша плоть не станет прозрачной”. Это потрясающая фраза, – говорит Макфарлейн. – Эти холмы никуда не спешат – так, по-моему, она говорит. Поэтому шорткаты – это абсолютная антитеза к этому способу достичь прозрения».
Однако Макфарлейн напомнил мне, что многие из троп, по которым мы сегодня гуляем ради собственного удовольствия, впервые были проложены в неолитические времена именно в качестве шорткатов. Жизнь в скудных условиях вынуждала людей соизмерять затраты энергии, имеющиеся ресурсы и так далее. Когда они находили короткую дорогу, то вряд ли пренебрегали ею – независимо от того, открывались ли на ней такие же возможности для созерцания, как и на длинной, или нет.
Но не всегда. Как отмечает Макфарлейн, иногда неолитические культуры тратили огромное количество ресурсов на проекты, не сводящиеся к пользе для выживания. В качестве иллюстрации к этому тезису он рассказал мне прекрасную историю о рубилах, которые добывали в долине Литл-Лэнгдейл в камберлендском Озерном крае. Она показывает, что не все неолитические тропы служили рациональными шорткатами: «На нижних уровнях этой долины были прекрасные скальные выходы подходящей для рубил породы, которые вполне можно было бы использовать для изготовления инструментов – стоило только захотеть. Но они явно предпочитали забираться на гораздо более высокие и труднодоступные площадки на утесе Гиммер-Крэг».
Мне стало любопытно, почему люди шли в труднодоступные места за той же самой породой, которую можно было добыть гораздо легче.
«У мест есть особая аура, которая остается в предмете после того, как его забирают из такого места, – сказал он. – Так что и в доисторические времена люди выбирали не только короткие, но и длинные пути не без причины».
Затем Макфарлейн отплатил мне той же монетой. Есть ли в математике примеры необычайно плодотворных длинных путей?