Развернем цилиндр – и у нас получится карта. Таким способом невозможно изобразить на карте полюса, так что на верхнем крае карты оказывается параллель, близкая к полюсу[74]. Такая карта все сильнее растягивает параллели по мере продвижения на север или на юг от экватора. Для тех, кто был в море, она была великолепным инструментом, к чему, видимо, и стремился Меркатор, ибо он дал своей карте следующее название: «Новое и более полное описание земного шара, должным образом приспособленное для использования в навигации» (Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendate Accommodata, 1569).
Хотя на этой карте сохраняются углы между линиями, проведенными на глобусе, этого не происходит с площадями и расстояниями. И это обстоятельство имело очень важные политические последствия. Карта была настолько полезна, что в течение столетий она оставалась общепризнанным представлением о том, как выглядит наша планета. Но на ней чрезвычайно сильно преувеличено место, которое занимают страны, удаленные от экватора, – к примеру, Нидерланды и Великобритания. Например, если начертить круг на экваторе и другой круг такого же размера в Гренландии, в проекции Меркатора площадь второго круга увеличится в десять раз. Скажем, Африка на карте имеет те же размеры, что и Гренландия, хотя на самом деле она в 14 раз больше по площади.
Карта Меркатора противоречила политическим соображениям постколониальной эпохи, и вместо нее ЮНЕСКО приняло в качестве официальной альтернативную проекцию, которая называется проекцией Галла – Петерса. Эту карту широко используют в британских школах, но в школах Соединенных Штатов – в Бостонском школьном округе – она заменила карту Меркатора лишь в 2017 году. Многие другие американские школьные округа так и не последовали этому примеру. Многим гражданам Соединенных Штатов кажется, что уменьшение размеров США не согласуется с тем местом, которое их страна занимает на мировой арене.
По правде говоря, в любой карте неизбежны компромиссы. Собственно говоря, это обстоятельство открыл Гаусс, когда исследовал природу кривизны разных геометрий. Он назвал свое открытие «Theorema Egregium», то есть «Замечательной теоремой»: в ней он доказал, что плоской картой невозможно обернуть сферический глобус без искажения расстояний. На любой карте планеты приходится жертвовать чем-нибудь. Карта Галла – Петерса точно отражает площади, но не формы стран. Длина Африки получается вдвое большей ее ширины, тогда как на самом деле форма этого континента ближе к квадратной.
Разумеется, на большинстве карт Северное полушарие всегда находится вверху, а Южное – внизу. Но сферы симметричны, так что нет никаких причин, по которым карта не может быть ориентирована наоборот. Выбор ориентации опять-таки отражает то обстоятельство, что карты составляли обитатели Северного полушария.
Австралиец Стюарт Макартур решил противопоставить такому перевесу севера свою собственную карту, в которой Южное полушарие находится наверху. Тех, кто видит ее в первый раз, эта карта приводит в сильное замешательство. Кажется, что в ней что-то не так. Но это всего лишь показывает, насколько мы привыкли видеть планету с точки зрения Меркатора.
Самое главное в карте – то, чего мы хотим добиться с ее помощью. Нужен шорткат для навигации? Шорткат к пониманию размеров территории? Чаще всего на картах стараются точно воспроизвести какие-нибудь геометрические параметры. Например, размеры на карте могут соответствовать размерам на планете. Или же могут совпадать углы между линиями. Но бывает и так, что карта отбрасывает все эти полезные вещи и сохраняет лишь информацию, самую важную для перемещения из пункта А в пункт Б.
Одна из карт, которые я люблю больше всего и использую ежедневно, – это схема лондонского метро. Физическая карта, на которой показано географическое расположение станций и линий метро, не очень-то помогает перемещаться по городу. Вместо этого легендарная схема Гарри Бека, опубликованная в 1933 году, показывает, как связаны элементы этой сети, игнорируя физические расстояния. Эта карта была настолько революционной, что поначалу компания, управлявшая метрополитеном, ее отвергла. Проблема, однако, состояла в том, что компания несла убытки, так как лондонцы не пользовались ее системой. Когда попытались выяснить, почему это происходит, оказалось, что пассажиры просто не могли разобраться в сети. Карты, разработанные компанией, пытались воспроизводить географию города, но в результате получалась невразумительная, запутанная мешанина линий, в которой было трудно что-либо понять.
Бек осознал эту проблему и решил, что от географической точности следует отказаться. Он переместил линии, выпрямил их, подвел их к пересадочным станциям под ясными углами, отодвинул станции друг от друга. Возможно, Беку помог опыт работы в области электроники, потому что схема метро получилась больше похожей на электронную схему, чем на железнодорожную карту.
Поняв, что необходима более удобная карта, позволяющая пассажирам ориентироваться в сети линий метро, компания в конце концов решила принять проект Бека. Три четверти миллиона экземпляров его схемы были отпечатаны и розданы пассажирам. Схема завоевала всемирную славу. По ее мотивам создавали произведения искусства: в отделе современного искусства Британской галереи Тейт висит картина Саймона Паттерсона, на которой воспроизведена схема метро, но названия станций заменены на имена инженеров, философов, путешественников, планет, журналистов, футболистов, музыкантов, киноактеров, святых, итальянских художников, синологов (китаеведов), юмористов и «Людовиков» (французских королей). Дж. К. Роулинг даже придала форму этой схемы шраму на левом колене профессора Дамбльдора, намекая на то обстоятельство, что самые лучшие идеи, которые она использовала в книгах о Гарри Поттере, приходили ей в голову в поездах.
Преимущество схемы лондонского метро заключается в том, что она – не географическая карта; она сосредоточена на более важной задаче – показать, как добраться из точки А в точку Б. То, что участок между станциями Ковент-Гарден и Лейстер-сквер имеет на схеме такую же длину, как участок между Кингс-Кросс и Каледониан-роуд[75], не означает, что соответствующие расстояния одинаковы. Пассажиру гораздо важнее понимать, что эти станции соединены линией метро, чем знать, на каком расстоянии друг от друга они находятся.
Это пример нового мировоззрения, появившегося в середине XIX века. Точные расстояния между объектами могут не иметь значения; главным фактором, определяющим форму, часто бывают связи между этими объектами. Одним из первых исследователей, которые начали задумываться о том, что свойства поверхностей могут зависеть не столько от физической геометрии, сколько от связей между точками, расположенными на них, был Гаусс. Хотя он так и не опубликовал свои идеи, они послужили отправной точкой для работ Иоганна Бенедикта Листинга, впервые назвавшего в 1847 году этот новый способ видения мира топологией. В главе 9 мы увидим, что топологические карты могут быть чрезвычайно удобным шорткатом к ориентированию в самых разных сетях, не только в лондонском метро.
Но диаграммы не обязательно ограничиваются иллюстрированием физических связей между разными точками Лондона. Очень эффективно используются карты, на которых отмечают не станции метро, а идеи. Их называют картами мыслей[76], а их назначение – выявить интересные связи между разными идеями, которые мы исследуем. Карты мыслей уже много лет служат незаменимой подмогой студентам, зубрящим перед экзаменами, потому что они помогают превращать темы, которые кажутся слишком сложными для выражения словами, в связные повествования. В известном смысле они опираются на принцип дворца памяти, о котором рассказывал Эд Кук. Карта мыслей может преобразовать винегрет из идей в воображаемый маршрут, по которому можно путешествовать по страницам.
Однако у этих диаграмм долгая история. Студентом в Кембридже Ньютон рисовал в записных книжках загогулины, складывающиеся в своего рода карту мыслей, которой он иллюстрировал свои идеи о возможных связях между разными философскими вопросами. Суть в том, что такие карты нарушают более или менее линейную манеру, в которой идеи обычно бывают представлены в учебниках, имитируя более многомерные процессы, которые использует для обработки идей наш разум.
Отображение великого и малого
Как говорил Леонардо, визуальный мир способен описать то, что навсегда останется недоступным для мира письменного. Одно-единственное изображение может выразить основополагающую структуру, которую скрывает сложность слов или уравнений. Но диаграмма – это не просто физическое представление того, что мы видим глазом. Могущество диаграмм заключается в их способности кристаллизовать новые способы видения мира. Как показывает шуточная идея Кэрролла о безмасштабной карте, для этого часто требуется отбросить часть информации, сосредоточиться лишь на самом главном. В других случаях научные идеи переводятся на язык визуальных образов, создающий новую карту, в которой главную роль играют геометрические построения, помогающие нам разобраться в том научном вопросе, о котором идет речь.
Силу хорошего изображения, несомненно, сознавал польский математик и астроном Николай Коперник. Изложение гелиоцентрической теории Коперника занимает в его великом труде, трактате «О вращении небесных сфер» (De revolutionibus orbium coelestium), опубликованном незадолго до его смерти в 1543 году, 405 страниц текста, чисел и формул. Однако лучше всего его революционную идею – что центром Солнечной системы является не Земля, а Солнце – выражает простое изображение, схема, которую Коперник начертил в самом начале этой книги.
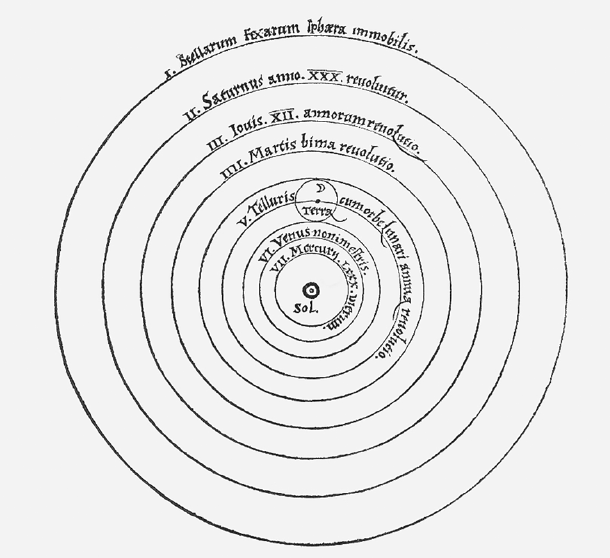
Рис. 5.6. Схема Солнечной системы, в центре которой находится Солнце, из книги Коперника
В его иллюстрации присутствуют некоторые из важнейших элементов лучших диаграмм. Не предполагается, что концентрические окружности точно описывают орбиты планет. Коперник знал, что форма орбит отличается от окружности. Не предполагается, что одинаковые расстояния между окружностями показывают, насколько планеты удалены от Солнца или друг от друга. Этот чертеж всего лишь выражает простую, но потрясающую мысль о том, что мы находимся не в центре всего. Он преобразил наши взгляды на то место, которое мы занимаем во Вселенной.
Сегодня космологи используют диаграммы для изображения всей Вселенной и всех 13,8 миллиарда лет ее истории, для представления строения массивных черных дыр, для понимания сложных аспектов нашего четырехмерного пространства-времени. Присущая диаграммам способность открывать шорткаты к огромности Вселенной – это, пожалуй, единственный способ, которым мы можем осознать свое место на масштабе, кажущемся на первый взгляд невозможно большим.