К тому времени Галилей уже открыл формулу, позволяющую установить, какое расстояние яблоко пролетает за любой временной промежуток. За
Возьмем яблоко и подбросим его вертикально вверх. Предположим, я бросил его со скоростью 25 метров в секунду. У бейсболистов, подающих мячи, скорость броска может превышать 40 метров в секунду, так что моя цифра не выходит за пределы разумного. Теперь высота положения яблока после броска определяется по формуле 25
При помощи этой формулы я могу рассчитать, через какое время яблоко снова долетит до моей руки, то есть его высота над моей рукой, равная 25
Но Ньютон хотел найти способ узнавать, какова скорость полета яблока в каждой точке его траектории. Однако эта скорость непрерывно изменяется, так как яблоко сперва замедляется, а затем снова ускоряется.
Попробуем вычислить при помощи нашей формулы – отношения пройденного расстояния ко времени, за которое это расстояние было пройдено, – скорость через 3 секунды. Итак, расстояние, которое пролетает яблоко между 3-й и 4-й секундами, равно
(25 × 4 – 5 × 42) – (25 × 3 – 5 × 32) = 20 – 30 = –10 м.
Минус показывает, что яблоко летит в направлении, противоположном тому, в котором я его бросил. Оно уже падает вниз. Таким образом, средняя скорость за этот период равна 10 метрам в секунду. Но это лишь средняя скорость за интервал длительностью в одну секунду. Она не равна действительной скорости яблока через 3 секунды после броска. Может быть, попробовать взять меньший интервал? Если делать этот интервал все меньше, оказывается, что скорость становится все ближе и ближе к 5 метрам в секунду. Но Ньютон хотел получить скорость моментальную, соответствующую нулевому временному промежутку. Его метод дал возможность понять, почему моментальная скорость через 3 секунды должна быть равна 5 метрам в секунду.
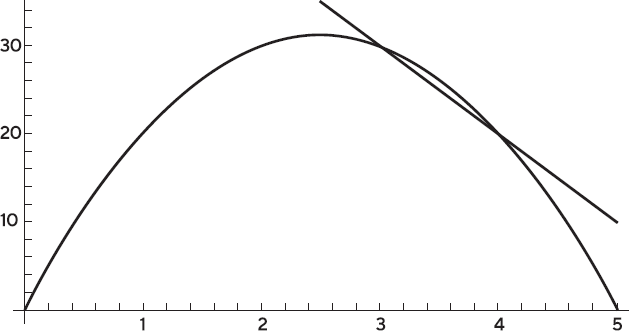
Рис. 6.2. График зависимости высоты полета яблока от времени. Средняя скорость между двумя значениями времени равна наклону прямой, проведенной через соответствующие точки графика
Скорость можно представить на графике зависимости пройденного расстояния от времени. Средняя скорость между 3-й и 4-й секундами – это наклон прямой, проведенной между двумя точками графика, соответствующими 3-й и 4-й секундам. Если уменьшать этот интервал, прямая будет приближаться к кривой, пока не попадет в положение, в котором она лишь касается ее в точке
25 – 10
Вот почему это так: предположим, мы хотим вычислить скорость в момент
(25(
Теперь разделим на величину временного интервала
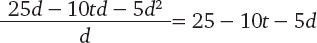
Если взять чрезвычайно малую величину
25 – 10
Это выражение называется производной функции 25
Производителю важно знать стоимость создания новой продукции, чтобы установить цену, которая будет обеспечивать прибыль. Вначале себестоимость продукции будет очень высокой из-за расходов на оборудование производства, наем работников и так далее. Но по мере производства все больших ее объемов себестоимость каждого следующего изделия будет изменяться. Вначале она будет снижаться, потому что производство этой продукции будет становиться все более экономичным. Но если чрезмерно увеличить объемы производства, стоимость продукции снова может вырасти. Увеличение производства рано или поздно приводит к работе в сверхурочное время, использованию менее производительных старых предприятий, конкуренции за дефицитное сырье и тому подобному. В результате стоимость дополнительных изделий увеличивается.
Это несколько похоже на подбрасывание в воздух мяча: сначала мяч летит быстро, но с каждой следующей секундой замедляется и пролетает все меньшее расстояние. Математический анализ может помочь производителю понять, как себестоимость продукции изменяется с изменениями объема производства, и найти оптимальную точку, то есть узнать, сколько нужно производить, чтобы себестоимость была наименьшей.
Открытый Ньютоном шорткат к пониманию подвижного мира положил начало современной науке. Я считаю Ньютона, как и Гаусса, одним из величайших мастеров шортката всех времен. Я даже совершил паломничество в поместье Вулсторп, где, как рассказывают, Ньютон сидел под яблоней, вдохновившей его на создание этого гениального шортката. К моему удивлению, дерево все еще было на месте! Мой экскурсовод позволил мне взять два его яблока, и из одного из их семечек мне удалось вырастить яблоню в своем саду. Под этим деревом я сижу долгими часами, надеясь найти шорткат, который приведет меня к решению задачи, над которой я сейчас работаю.
Гаусс, как и я, был горячим поклонником работ Ньютона. «Было всего три математика эпохального значения, – писал он, – Архимед, Ньютон и Эйзенштейн». Последнее имя – не опечатка. Речь идет о Готтхольде Эйзенштейне[89], молодом прусском ученом, занимавшемся теорией чисел. Он произвел на Гаусса столь сильное впечатление тем, что решил несколько задач, которые тот не смог решить сам.