Тригонометрия – шорткат к небесам

Древние греки применяли свою математику не только для измерения Земли. Они поняли, что ее можно использовать и для измерения небес. И важнейшим инструментом в этом деле были не телескопы или хитроумные рулетки, а математические средства тригонометрии.

Следы применения этих средств можно найти уже в вычислениях Эратосфена. Тригонометрия – это наука о треугольниках, объясняющая связи между углами треугольников и длинами их сторон. Этот раздел математики открыл перед математиками Античности необычайный шорткат, позволявший измерять космос, не покидая уютной поверхности Земли.

Например, еще в III веке до нашей эры Аристарх Самосский применил тригонометрию для вычисления отношения расстояния от Земли до Солнца к расстоянию от Земли до Луны. Для этого ему нужно было всего лишь измерить угол, образованный Луной, Землей и Солнцем, – тремя вершинами треугольника, – в день, когда Луна освещена ровно наполовину[50]. При этом угол, образованный Землей, Луной и Солнцем, составляет ровно 90 градусов (см. рис. 4.1). Затем, построив треугольник с измеренным углом, Аристарх мог рассчитать отношение расстояний от Земли до Луны и от Земли до Солнца, потому что оно равно отношению сторон меньшего треугольника, который он начертил. Хитрая идея состояла в том, что размеры треугольника значения не имеют: отношение всегда остается тем же самым. Это отношение называется косинусом угла, который измерял Аристарх.

Чтобы вычислить не отношение расстояний, а само расстояние, нужно измерить угол и длину одной из сторон треугольника. Хитроумный способ определения расстояний от Земли до Луны и Солнца открыл Гиппарх, которого традиционно называют первооснователем тригонометрии. Он воспользовался несколькими солнечными и лунными затмениями, в частности солнечным затмением, наблюдавшимся 14 марта 190 года до нашей эры.

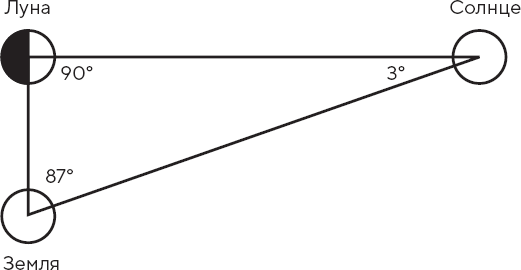
Рис. 4.1. Измерение расстояний в Солнечной системе при помощи треугольников

Как и Эратосфен, Гиппарх использовал две разные точки на поверхности Земли. На Геллеспонте[51] затмение было полным, а в Александрии – лишь частичным: там Луна закрывала только четыре пятых Солнца. Благодаря этому Гиппарх, подобно Эратосфену, получил расстояние, которое он мог измерить на Земле. Сочетание расстояния между двумя точками с измеренными углами, под которыми было видно затмение, позволило ему вычислить расстояние от Земли до Луны тригонометрическими методами.

Этот тригонометрический шорткат давал поразительные возможности. Он побудил Гиппарха начать подготовку первого в истории примера тригонометрических таблиц. В них можно было взять какой-нибудь угол и найти отношение длин сторон прямоугольного треугольника, содержащего такой угол. Даже здесь математики открыли шорткаты, избавляющие их от необходимости строить множество треугольников и измерять длины сторон и величины углов каждого из них.

Возьмем, например, равносторонний треугольник: все его стороны одинаковы, а все углы равны 60 градусам. Проведем из одной из его вершин линию, делящую угол при этой вершине на два угла по 30 градусов и образующую с основанием угол 90 градусов. Косинус угла 60 градусов – это отношение длин сторон, образующих этот угол во вновь построенном прямоугольном треугольнике. Легко видеть, что он равен 1/2, потому что длина катета этого нового треугольника равна половине длины стороны исходного равностороннего треугольника.

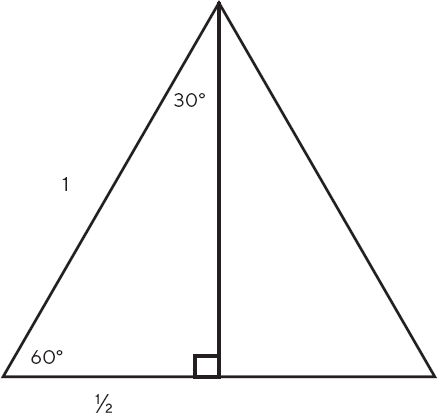
Рис. 4.2. Косинус 60°

Но математики открыли и изящную формулу, связывающую косинусы углов одного треугольника с косинусами углов треугольника, содержащего угол, вдвое меньший. Это дает нам возможность вычислять и другие величины.

cos² x = 1/2 + 1/2 cos (2 x)

При помощи этих шорткатов можно составить таблицы косинусов множества разных углов. Именно эти таблицы стали самым действенным измерительным средством для исследования ночного неба. Они же сыграли ключевую роль в прокладывании шорткатов к измерениям на Земле. Их наверняка использовал при проведении геодезических съемок Ганновера и Гаусс. Землемеры до сих пор пользуются этим математическим шорткатом к измерениям.

Например, если вы хотите узнать высоту дерева, измерять ее от корней до вершины складным метром будет делом довольно трудным. Вместо этого геодезист отходит от дерева на некоторое расстояние и измеряет, под каким углом проходит прямая, соединяющая почву с вершиной дерева. Произведя гораздо более простое измерение расстояния между геодезистом и основанием дерева и найдя в таблицах тангенс нужного угла (величину, выражающую отношение длин двух коротких сторон треугольника[52], в данном случае – высоты дерева и расстояния от его основания до геодезиста), геодезист может найти высоту дерева, не залезая ни на какую лестницу.

Красивую демонстрацию способностей тригонометрии по части создания шорткатов дает история измерения метра. Можно подумать, что измерение метра – дело довольно странное, поскольку метр и есть единица измерения. Но история эта начинается с определения того, что такое, собственно говоря, метр.

Измерение метра

С тех самых пор, когда первые древние цивилизации начали строить города, нам понадобились единицы измерения, помогающие вести строительство согласованно. Первые варианты таких единиц появились еще у древних египтян, которые ориентировались на части тела. Локтем называлось расстояние от локтя до кончика среднего пальца. Такая же привязка к частям тела ясно видна в единицах измерения, бытовавших до введения метрической системы. Фут, разумеется, соответствовал длине ступни[53]. Дюйм во многих европейских языках называется тем же словом, что и большой палец[54]. Ярд тесно связан с длиной человеческого шага. Интересно отметить, что единицу под названием «род», которую использовали для измерения земли в саксонские времена, определяли следующим образом: это суммарная длина левых ступней первых 16 человек, вышедших из церкви воскресным утром. Однако размеры и формы тела людей настолько разнятся, что и результаты таких измерений должны получаться чрезвычайно непостоянными.

Король Генрих I попытался решить эту проблему, распорядившись сделать эталоном для стандартизации этих единиц измерения королевское тело. Он постановил, что ярдом следует считать расстояние от кончика носа короля до кончика большого пальца его вытянутой руки. Но и у этого решения, разумеется, были свои недостатки, так как длина ярда могла изменяться каждый раз, когда на престол вступал новый монарх.

Вожди Французской революции полагали, что следует ввести эгалитарную систему измерений, доступную всем. Галилей доказал, что период колебаний маятника зависит от его длины, а не от веса или размаха колебаний. Сначала предложили считать метром длину маятника, колеблющегося с периодом две секунды. Однако выяснилось, что период колебаний зависит еще и от силы тяжести, которая бывает разной в разных точках мира.