Статистическая механика и термодинамика

Представьте себе заполненную воздухом емкость, в которой все молекулы хаотично движутся. Некоторые быстро, другие помедленнее. Но если в емкости поддерживаются одни и те же температура и давление, то общее количество содержащейся в ней энергии остается постоянным. Эта энергия распределяется между молекулами определенным образом: вся энергия рассредоточена согласно простому статистическому закону. Представьте, что мы вводим в емкость немного более теплого воздуха (более быстрые молекулы): случайные столкновения новых молекул с более прохладными «старожилами» перераспределят энергию. Одни молекулы замедлятся, а другие – ускорятся. В конечном счете молекулы опять стабилизируются в новом состоянии равновесия. На этот раз энергия любой молекулы будет с большой вероятностью несколько выше, чем ранее, а температура воздуха в емкости немного поднимется.

То, как энергия в емкости распределяется между молекулами, называется распределением Максвелла – Больцмана – в честь двух величайших ученых XIX века, которые и основали статистическую механику. Термин «распределение» относится к форме кривой, которая на графике показывает соотношение скорости и количества молекул, движущихся с этой скоростью. Или, иными словами, это линия, соединяющая точки, соответствующие степени вероятности того, что какая-то молекула движется с конкретной скоростью. Высшей точке на графике соответствует наиболее вероятная для молекул скорость, а более высокие или более низкие скорости являются менее вероятными. По мере увеличения температуры в емкости форма кривой изменяется, причем пик распределения вероятности сдвигается к более высоким скоростям. Когда распределение Максвелла – Больцмана восстанавливается, мы говорим, что воздух в емкости достиг термодинамического равновесия.

Стремление систем к статистическому состоянию равновесия связано с очень важным для физики понятием – энтропией. Энтропия системы при отсутствии постороннего воздействия всегда будет увеличиваться; то есть система будет выходить из «специфического» (упорядоченного) состояния и переходить в менее специфическое (смешанное) состояние. Физическим системам свойственно охлаждаться и изнашиваться. Это свойство называется вторым законом термодинамики, который, по сути, отражает не более чем статистическую неизбежность: при отсутствии внешнего воздействия все всегда возвращается к состоянию равновесия.

Представьте себе, что все молекулы воздуха в емкости изначально сконцентрированы в одном ее углу. В начальном состоянии энтропия в емкости низка, поскольку молекулы в ней пребывают в особом, более упорядоченном состоянии. При отсутствии воздействия извне молекулы из-за произвольного движения быстро распределятся по всей емкости – распределение станет равновесным. Так же как скорость нагретых молекул в конце концов снижается до значений, соответствующих состоянию термодинамического равновесия, молекулы в емкости по мере распространения равновесия переходят из состояния низкой в состояние высокой энтропии. Когда молекулы воздуха равномерно распределятся по емкости, энтропия достигнет своего максимума.

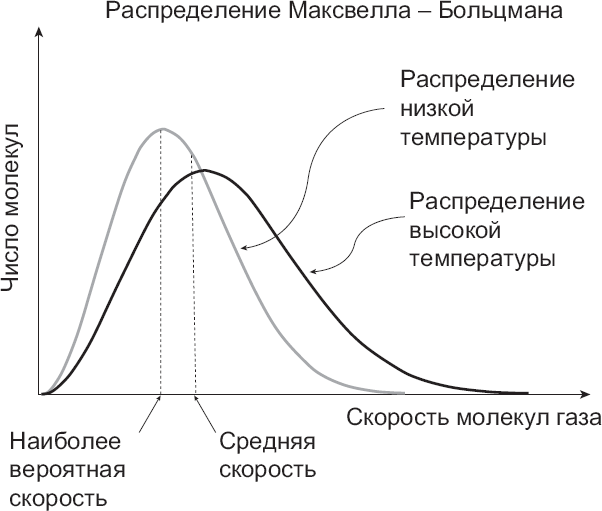
Рис. 2. Распределение Максвелла – Больцмана: молекулы газа в емкости будут равномерно распределяться и делиться энергией, пока не достигнут теплового равновесия. Кривая, отражающая количество молекул по отношению к их скорости, известна под названием распределения Максвелла – Больцмана, и пик ее обозначает самую вероятную скорость. По мере возрастания температуры газа этот пик сдвигается к более высокой скорости. Отмечу, что самая вероятная скорость – это не то же самое, что средняя скорость, поскольку в емкости есть частицы со скоростями выше пиковой величины

А вот еще более простой пример. Упорядоченная колода карт, в которой каждая масть сложена отдельно в восходящем порядке, как мы говорим, имеет низкую энтропию. Это в высшей степени упорядоченное состояние, которое нарушается, когда мы тасуем колоду, – и мы говорим, что энтропия увеличивается. Когда мы перемешиваем колоду далее, более вероятно, что порядок еще больше нарушится, чем что карты вернутся в свое первоначальное упорядоченное состояние. Так происходит потому, что в неперемешанной колоде карты сложены в уникальном порядке, тогда как вариантов перемешанной существует бесчисленное множество. Поэтому гораздо более вероятно, что перемешивание пойдет в одном направлении – от неперемешанного состояния к перемешанному, от низкой энтропии к высокой.

Более интересное определение энтропии – следующее: это мера способности объекта затрачивать энергию на осуществление какой-либо задачи. Когда система достигает равновесия, она становится бесполезной. Полностью заряженный аккумулятор обладает низкой энтропией, которая увеличивается, когда его начинают использовать. И здесь в силу вступает различие между полезной и бесполезной энергией. Когда система упорядочена и находится в особом состоянии (с низкой энтропией), ее можно заставить осуществлять полезную работу – так происходит с заряженным аккумулятором, заведенными часами, солнечным светом, химическими связями между атомами углерода в куске угля. Но когда система приходит в равновесие, энтропия достигает максимума, а энергия, которой она обладает, становится бесполезной. Таким образом в некотором смысле для того, чтобы мир продолжал существовать, нужна не энергия, а низкая энтропия. Если бы все пребывало в состоянии равновесия, ничего бы не происходило. Для того чтобы заставить систему работать, то есть обеспечить переход энергии из одного состояния в другое, нужно, чтобы система находилась в состоянии низкой энтропии.

Жизнь – это система, которая может поддерживать себя в состоянии низкой энтропии вдали от теплового равновесия. По сути, живая клетка – сложная система, которая кормится (посредством тысяч биохимических процессов) полезной энергией с низкой энтропией, заключенной в молекулярной структуре пищи, которую мы поглощаем. Эта химическая энергия используется для того, чтобы поддерживать жизненные процессы. В конечном счете жизнь на Земле возможна только потому, что она поглощает энергию Солнца, обладающую низкой энтропией.

Второй закон термодинамики и неизбежная победа энтропии относится и ко всей Вселенной. Представьте себе, что наша емкость с воздухом теперь превратилась в облако холодного газа, расширившееся до размеров Галактики. Если несколько молекул в этом облаке случайно сблизятся на расстояние больше среднего, то очень слабого взаимного притяжения между ними может быть достаточно, чтобы притянуть их друг к другу и сформировать более плотный сгусток[23]. Чем больше молекул войдет в этот сгусток, тем более сильно будут притягиваться новые. Процесс формирования сгустков за счет притяжения лежит в основе образования звезд: огромные облака газа «спадались» воедино, пока не появлялись образования достаточно плотные, чтобы в них могла начаться термоядерная реакция, и тогда загорались звезды. Если задуматься, все это не совсем понятно, поскольку может показаться, что процесс образования сгустков приводит к формированию более упорядоченного, «особого» состояния, и поэтому конечное состояние должно иметь более низкую энтропию, чем когда все молекулы распределяются равномерным образом. Так что, неужели сила притяжения заставила энтропию газа понизиться, а второй закон термодинамики оказывается нарушенным?

Ответ: нет. Когда материя собирается в сгустки под воздействием гравитации, ее энтропия увеличивается. Причина та же, что увеличение энтропии мячика, когда он скатывается с холма из-за силы притяжения Земли. Эти сгустки можно представить, как растянутую пружину, которую вдруг отпустили, или как часы, у которых кончается завод: по мере того как они теряют способность совершать полезную работу, их энтропия увеличивается. Таким образом, когда молекулы газа в определенной части облака случайно оказываются на время ближе друг к другу, чем при их равномерном распределении, это означает временный уход от максимальной энтропии. Чтобы энтропия снова увеличилась, по второму закону термодинамики эти молекулы могут сделать одно из двух. Они могут либо вновь разойтись в стороны друг от друга до своего прежнего состояния термального равновесия, либо вследствие действия взаимного притяжения, наоборот, собраться в сгустки. В любом случае их энтропия возрастет.

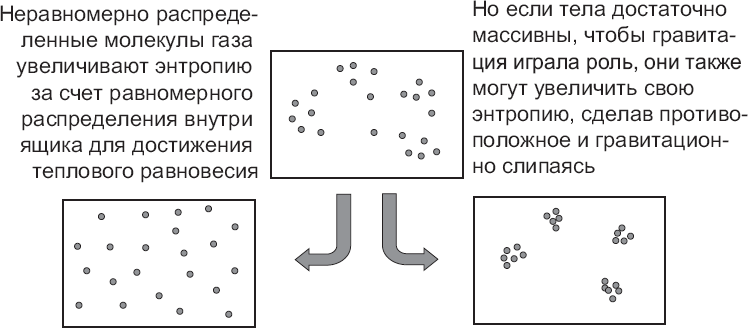
Рис. 3. Увеличение энтропии: частицы в емкости, которые слегка отошли от состояния равновесия (низкая энтропия), могут увеличивать свою энтропию либо путем перераспределения до достижения равновесия, либо путем образования сгустков под воздействием силы притяжения. В любом случае они повышают свою энтропию и следуют второму закону термодинамики

Теперь вам следует спросить: что же может вызвать такое отклонение от состояния максимальной энтропии? А дело в том, что материя и энергия в нашей Вселенной изначально находились не в состоянии термического равновесия, а в совершенно особом состоянии низкой энтропии, обусловленном самим Большим взрывом. Эти изначальные условия на квантовом уровне привели к возникновению в пространстве-времени огромного количества нарушений, которые начинали играть все большую роль в «космической ткани» по мере расширения Вселенной. Так что в процесс распределения материи была изначально заложена некоторая неравномерность. По мере того как Вселенная продолжала «раскручиваться», материя, которая была достаточно плотной, чтобы влияние притяжения оказалось значимым, в конце концов образовывала сгустки, а в дальнейшем – звезды и галактики. Молекулы водорода и гелия в космосе попадали в гравитационные колодцы, образуемые звездами, тем самым вызывая рост энтропии. Однако, что важно, эта энтропия не достигает максимума, поскольку звезды не находятся в состоянии термического равновесия, оставаясь, однако, резервуарами низкой энтропии, а термоядерные реакции в них высвобождают избыточную энергию в виде тепла и света. Именно такая энергия, исходящая от нашего Солнца, делает возможной жизнь на Земле. Растения используют ее в фотосинтезе для создания биомассы, накапливая полезную энергию с низкой энтропией в молекулярных связях органических соединений; затем ею могут воспользоваться другие живые существа, а в конечном счете и люди, которые поглощают растения в виде пищи.

Сама Земля тоже имеет запас полезной энергии, которая вместе с энергией Солнца определяет ее климат, тогда как гравитационная энергия Луны и Солнца управляет океанскими приливами. Все это обеспечивает полезные запасы низкой энтропии, которыми мы можем воспользоваться. Например, вода в верхней части водопада стекает под воздействием силы притяжения, превращая таким образом потенциальную энергию в кинетическую, которой мы можем пользоваться, построив гидроэлектростанции, генерирующие электричество. Конечно, всегда будет происходить некая потеря эффективности – согласно второму закону в целом необходим некоторый рост энтропии в виде бесполезного тепла.

Однако в мире происходит нечто гораздо более существенное, чем просто переход энергии из одной формы в другую.

Направленность времени

Если какая-либо физическая система, включая Вселенную, всегда развивается от упорядоченного состояния с низкой энтропией к неупорядоченному состоянию с высокой энтропией, то это нам задает направление течения самого времени: второй закон термодинамики позволяет нам различать прошлое и будущее. Это может показаться несколько странным; в конце концов, для того, чтобы понять, что вчера – это прошлое, нам не нужен второй закон термодинамики. В вашем мозгу хранится память о событиях этого дня, хотя сами события навсегда остались в прошлом. Между тем завтра неизвестно – ему еще предстоит произойти. Эта стрела времени, направленная из прошлого в будущее, как мы интуитивно чувствуем, является более фундаментальной принадлежностью реальности, а второй закон на нее опирается. А на самом деле все наоборот: второй закон термодинамики следует считать основой стрелы времени. Без второго закона не было бы ни будущего, ни прошлого.

Представьте себе, что мы смотрим фильм про нашу емкость с воздухом (а молекулы воздуха достаточно велики, чтобы мы могли их увидеть). Они будут метаться туда-сюда, сталкиваясь друг с другом и со стенами емкости, – некоторые побыстрее, другие помедленнее. Но если воздух находится в состоянии термического равновесия, то мы не сможем сказать, показывают ли нам фильм от начала к концу или от конца к началу. В масштабе молекулярных столкновений нам не удалось бы различить никакой направленности во времени. Без роста энтропии и стремления к равновесию все физические процессы во Вселенной могли бы с тем же успехом двигаться в обратном порядке. Однако, как мы видели, это стремление Вселенной и всего в ней к равновесию сводится к статистической вероятности событий на молекулярном уровне: от того, что может случиться с наименьшей вероятностью, к тому, что может случиться с большей, – согласно законам термодинамики. В направленности времени из прошлого в будущее нет ничего таинственного; это просто вопрос статистической неизбежности.

Если иметь это в виду, то даже тот факт, что я знаю прошлое, но не знаю будущего, больше не кажется странным. Когда я наблюдаю мир вокруг, увеличивается объем информации в своем мозгу – процесс, в ходе которого по мере работы моего мозга вырабатывается бесполезное тепло, а значит, растет энтропия моего тела. Даже сама наша способность различать прошлое и будущее с точки зрения термодинамики является не более чем проявлением второго закона в отношении нашего мозга.

Детерминизм и случайность