Но можем ли мы быть уверены, исходя из столь малого количества данных, что секрет подъема по лестнице действительно скрыт в числах Фибоначчи?
На самом деле правило точно объясняет, как вычислить количество вариантов для следующего этапа, лестницы из 6 ступенек. Нужно взять все возможные варианты для четырех ступенек и прибавить в конце по двойному шагу. Или взять все возможные варианты для пяти и прибавить к ним по шагу одинарному. Это дает все возможности для шести ступенек. Получается сочетание двух предыдущих чисел последовательности.
Чтобы получить ответ на исходную головоломку, нужно вычислить десятый член последовательности.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Существует 89 разных вариантов. Этот паттерн – шорткат к вычислению количества возможных способов подъема до вершины лестницы. И этот же паттерн позволяет решить эту задачу, даже если ступенек будет 100 или 1000.
Хотя эти числа названы в честь Фибоначчи, первым их открыл не он. Это были индийские музыканты, игравшие на табла[21]. Они издавна состязались друг с другом, щеголяя разными ритмами, которые им удавалось извлекать из своих барабанов. По мере исследования разных типов ритмов, которые получались из долгих и кратких тактов, они и пришли к числам Фибоначчи.
Если долгий такт в два раза длиннее краткого такта, то количество ритмов, которые может составить из них музыкант, играющий на табла, будет таким же, что и количество вариантов подъема по лестнице. Каждый одинарный шаг соответствует краткому такту, а каждый двойной шаг – долгому. Значит, число возможных ритмов определяется правилом Фибоначчи. Более того, это же правило дает музыканту алгоритм построения новых ритмов из уже существующих более коротких.
В том обстоятельстве, что один и тот же паттерн объясняет столь разнородные явления, есть нечто потрясающее. Фибоначчи полагал, что это закон роста в природе. С точки зрения индийских музыкантов, игравших на табла, этот паттерн порождает ритмы. Он же позволяет получить число вариантов подъема по лестнице одинарными и двойными шагами. Есть даже некоторые финансовые аналитики, считающие, что эти числа можно использовать для предсказания момента, в который падающий курс акций достигнет нижней точки и снова начнет расти. Этот финансовый паттерн не вполне бесспорен и уж точно не универсален, но некоторым инвесторам удается применять его для принятия правильных решений. Столь действенным делает шорткат способность выявить фундаментальную структуру, скрытую за самыми разными фасадами. Один и тот же паттерн может дать решения множеству кажущихся совершенно разными задач. Когда приступаешь к решению новой задачи, часто бывает полезно проверить, не сводится ли она к старой задаче, решение которой вы уже нашли.
Связи между шорткатами
Я не могу противостоять искушению прибавить к этой истории небольшой эпилог, в котором пожинаются плоды проделанной ранее тяжелой работы. Моя исходная стратегия вычисления количества способов подъема на вершину лестницы привела меня к вопросу о способах выбора 3 предметов из 7. На самом деле математики уже нашли хитроумный метод, укорачивающий путь к вычислению этих вариантов. Он называется треугольником Паскаля (хотя, как и в случае Фибоначчи, оказывается, что первым его открыл вовсе не Паскаль: это заслуга древних китайцев).
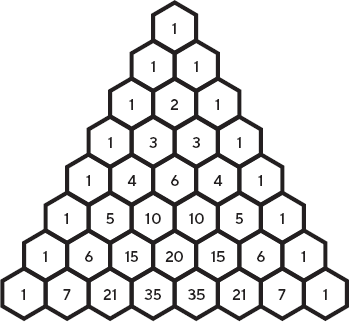
Рис. 1.5. Треугольник Паскаля
Треугольник этот строится по правилу, похожему на правило Фибоначчи, но в этом случае каждый элемент нижележащего ряда вычисляется как сумма двух элементов, расположенных над ним. Используя это правило, построить треугольник легко, но замечательнее всего то, что он содержит все те интересные числа, которые я искал. Предположим, я заведую пиццерией и хочу похвастаться количеством разных пицц, которые у меня можно заказать. Если мне нужно узнать число вариантов выбора 3 начинок из 7 возможных, я беру (3 + 1) – е число в (7 + 1) – м ряду треугольника: 35. Этот шорткат показывает мне, что я могу приготовить 35 разных пицц. В общем случае выбора
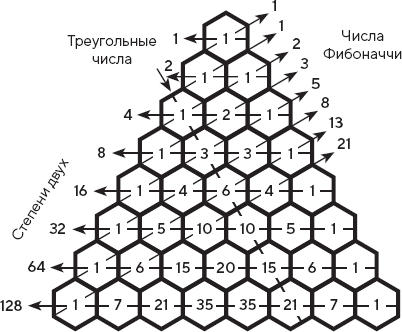
Рис. 1.6. Числа Фибоначчи, треугольные числа и степени двух в треугольнике Паскаля
Связи такого рода – одна из тех вещей, которые я особенно люблю в математике. Кто бы мог подумать, что в треугольнике Паскаля прячутся числа Фибоначчи? Однако, рассмотрев нашу головоломку двумя разными способами, я нашел тайный туннель, шорткат, соединяющий эти, казалось бы, совершенно разные уголки математического мира! А кроме того, оказывается, что в треугольнике спрятаны еще и треугольные числа и степени двойки. Треугольные числа находятся на одной из диагоналей треугольника, а степени двух получаются суммированием всех чисел каждого ряда. В математике полно таких странных туннелей, открывающих перед нами шорткаты, которые мы можем использовать для превращения одних объектов в другие.
Обнаружение паттернов в данных нужно не только для решения занятных задачек о способах подъема по лестницам и тому подобном. Оно является ключевым элементом предсказания развития Вселенной, и Гаусс убедился в этом, когда предсказал траекторию движения Цереры. Это жизненно важный фактор понимания изменений климата. Оно играет центральную роль в помощи компаниям, пытающимся разобраться в неопределенностях будущего. Возможно, оно даже может дать нам некоторые представления о ходе истории человечества. В наше невероятно богатое данными время в интернете каждый день производится один эксабайт (1018 байт) данных. Это огромное количество чисел, требующих анализа. Но, если заметить в них паттерн, можно найти шорткат к ориентации в этом колоссальном цифровом мире.
Шорткаты на основе паттернов сводятся к выявлению правил или алгоритмов, лежащих в основе производства данных, в которых вы хотите разобраться. Шорткаты этого типа продолжают работать, даже когда масштабы задачи, казалось бы, неконтролируемо увеличиваются. Лестница может становиться все длиннее и длиннее, но шорткат по-прежнему приводит к ответу.
Однако паттерны касаются не только чисел. Во многих областях жизни есть паттерны, которые мы можем использовать для переноса понимания из одной дисциплины в другую. Например, понимание паттернов музыки – важнейшая часть обучения игре на музыкальных инструментах. Всемирно известная виолончелистка Натали Клейн считает, что паттерны музыкальных произведений помогают ей предсказывать направление, в котором может развиваться та или иная пьеса, еще до того, как она дочитает нотную запись.
В дальнейшем у меня будет возможность поговорить о шорткатах в психотерапии со Сьюзи Орбах. Оказывается, она использует множество паттернов человеческого поведения. Она может опираться на паттерны, о которых узнала в процессе работы с предыдущими пациентами, в помощи новым обращающимся к ней пациентам. Но люди – существа несколько более беспорядочные и своеобразные, чем числа, так что с этими паттернами, о которых расскажет Орбах, следует обращаться с осторожностью. Лучше всего паттерны работают, когда мир выражается в числах, что все чаще и чаще происходит в нашем цифровом мире. Наши цифровые отпечатки все в большей степени преобразуют наше человеческое поведение в числа. Стоит найти в этих числах паттерн, и перед вами открывается шорткат к возможности предсказания будущих действий человека.
Шорткат к шорткатам
Обнаружение паттернов – это поразительный шорткат к пониманию будущего. Если вы обнаружите паттерн в биржевых курсах, это может дать вам преимущество, когда вы займетесь инвестициями. Где бы вы ни сталкивались с числами, ищите в данных скрытые паттерны. Но паттерны бывают не только в числах. Они есть и у людей. Если вы заметите паттерн в ударах своего противника по игре в теннис, вы будете готовы к его следующему обводящему удару. Если вы поймете паттерны в пищевых привычках посетителей своего ресторана, вы сможете кормить их, не производя чрезмерного количества отходов и не создавая запасов невостребованной еды. Выискивание паттернов было основополагающим шорткатом человечества с тех самых пор, как мы начали делать первые шаги из своей саванны.