Однако, несмотря на все эти полезные способы работать с музыкой, в сущности, по мнению Клейн, в том, чем она занимается, не бывает шорткатов: «Для того, кто хочет стать профессиональным виолончелистом, особенно заниматься сольными выступлениями, получить известность, ощущать, что твою работу внимательно изучают, – ничего такого нет. Никаких шорткатов. И именно это мне и нравится. Как известно, Пабло Казальс упражнялся всю жизнь, и когда ему было девяносто пять, его спросили: “Маэстро, почему вы все еще продолжаете упражняться?” – и он ответил: “Потому что мне кажется, что у меня наконец начинает что-то получаться. Я совершенствуюсь”. По-моему, именно это побуждает продолжать работать. Нужно много тяжелого труда, и легче не становится. Чтобы работать всю жизнь, нужно увлекаться своим делом. Невозможно достичь самой высокой вершины».
Именно поэтому многих специалистов не слишком беспокоят шорткаты. Клейн сказала мне: «Идея шортката кажется привлекательной в краткосрочной перспективе, но не в долгосрочной. Я думаю, если бы было много шорткатов, задачи не казались бы нам такими же интересными».
Я признаю, что между стремлением достичь цели и легкостью, с которой это можно сделать, есть некое противоречие. Если задача оказывается слишком легкой, ее решение не приносит удовлетворения. И все же я не хочу заниматься бездумной, монотонной работой. Самое большое удовольствие я получаю именно от тех шорткатов, которые открываются после того, как я некоторое время топчусь на месте, не зная, удастся ли мне вообще добраться до цели. Выбросы адреналина в те моменты, когда становится виден хитроумный путь к решению, – это моя страсть, которая разгоралась по мере совершенствования моего математического мастерства. Но в том, что касается виолончели, я понимаю: хотя некоторые паттерны могут быть полезны, никаких шорткатов, избавляющих от тяжелой работы, тут не существует.
2
Шорткаты вычислительные
Вы – бакалейщик и хотите взвешивать товары от 1 до 40 килограммов на простейших равноплечных весах. Каково минимальное число гирь, необходимых для этого, и какого они должны быть номинала?
Удобный шорткат для выражения какой-нибудь идеи бывает мощным средством ускорения мысли. Тот способ, которым я могу выразить концепцию миллиона при помощи всего лишь семи символов – 1000000, – кажется мне само собой разумеющимся. Но в этих семи символах скрыта целая история поразительно интересных шорткатов, помогающих рационально разбираться в числах и вычислять. В течение всей истории человечества – и даже сейчас, если речь идет о коммерции, строительстве или банковском деле, – те, кому удавалось вычислить ответ быстрее и рациональнее, чем конкурентам, получали преимущество. В этой главе я хочу рассказать о некоторых хитроумных способах, которые мы изобрели для работы с числами и вычислений. Интересно отметить, что эти шорткаты могут быть действенными стратегиями даже там, где речь идет вовсе не о числах.
Многие думают, что раз я работаю в области фундаментальной математики, я, наверное, занимаюсь делением в столбик, вычисляя множество знаков после запятой. Неужели мое рабочее место еще не занял электронный калькулятор? Такое ошибочное представление, что математики – это такие сверхвычислители, встречается часто. Но это вовсе не значит, что в моей работе нет вычислений. Многие изощренные математические темы начинались с задач, требовавших изобретения хитроумных арифметических методов, – как это было с шорткатом, который нашел в школе Карл Фридрих Гаусс. Существует богатая история шорткатов, которые открыли люди, пытавшиеся считать более рационально. Даже калькуляторы, которыми мы пользуемся сегодня, были запрограммированы с учетом некоторых из наиболее удачных шорткатов, придуманных на протяжении многих лет математиками.
Мы привыкли считать компьютеры всемогущими устройствами, способными сделать что угодно. Но возможности компьютеров тоже небезграничны. Взять хотя бы задачу о сложении чисел до 100, которую решал Гаусс. Разумеется, компьютер справится с ней без всякого труда. Однако бывают числа, слишком большие даже для компьютера. Если попросить его сложить все числа, меньшие такого числа, он зависнет. В целом компьютерам по-прежнему нужны люди, придумывающие шорткаты, которые, будучи вставлены в компьютерные программы, позволяют машинам делать больше и быстрее. В этой главе я расскажу о довольно поразительном применении одной на первый взгляд заумной математической идеи – мнимых чисел, – открывшем очень важный шорткат, который позволяет компьютерам решать множество самых разных задач, в том числе сажать самолеты достаточно быстро, чтобы они не сталкивались в воздухе.
Шорткат к счету
Уже то, как именно мы записываем числа, может определить, будут ли вычисления простыми или окажутся сложной и трудной работой, в которой легко ошибиться. Момент, когда мы поняли, что удобное символическое обозначение сложных идей – это шорткат к эффективному мышлению, был важным моментом развития человечества. Судя по историческим данным, каждая цивилизация осознавала, что письменность вообще и записывание устной речи в частности дает мощное средство для сохранения, передачи и использования новых идей. И каждый раз при возникновении новой системы письменности какого-либо языка, как правило, появлялись и новые хитроумные способы записи концепции чисел. Но те цивилизации, которые создавали более удобные системы записи чисел, получали в свое распоряжение шорткаты к более быстрым и рациональным методам вычислений и работы с данными.
Одним из самых первых шорткатов, открытых математиками, было удобство позиционной системы счисления. Когда вы считаете что-нибудь, будь то овцы или дни, в первую очередь вам может прийти в голову идея пометить каждую овцу или каждый день особым символом. По-видимому, именно так и считали первые люди. Имеются кости с зарубками, сделанными 40 000 лет назад, которые считают примером первых попыток счета.
Уже это достижение было важным. Оно отмечает начало зарождения абстрактной концепции чисел. Археологи не знают, что именно подсчитывали при помощи этих зарубок, но у людей уже было понимание, что у их количества и количества овец или дней, что бы они там ни считали, есть нечто общее. Проблема состоит в том, что отличить 17 от 18 в записи, сделанной зарубками на кости, может быть довольно непросто. Нужно заново пересчитать все зарубки. В какой-то момент почти в каждой культуре возникает светлая идея создания некой сокращенной, более удобной для чтения записи всех этих зарубок.
Несколько лет назад, когда я жил в Гватемале, меня заинтриговали странные последовательности точек и тире, встречавшиеся на тамошних банкнотах. Я спросил нашу соседку, не закодированы ли в местных деньгах надписи какой-то странной азбукой Морзе. Она объяснила, что это действительно код, но закодирован на каждой банкноте ее номинал. Точки и тире были сокращенным представлением способа записи чисел, существовавшим в культуре майя. Майя понимали, что человеческому мозгу трудно определять количество зарубок, когда их больше четырех. Поэтому они не ставили на странице все больше и больше точек, а, дойдя до пяти, проводили через четыре точки линию – как делают заключенные, считающие дни до выхода на свободу. Таким образом линия стала условным обозначением числа пять.
Но что делать, если нужно сосчитать еще большее количество? Древние египтяне разработали весьма впечатляющую систему иероглифов, обозначающих разные степени десяти. Число десять обозначалось изображением пут для скота (приспособления, ограничивающего движения животного), сто – веревочной петлей, тысяча – цветком кувшинки, десять тысяч – согнутым пальцем, сто тысяч – лягушкой и, наконец, миллион – коленопреклоненным человеком с воздетыми к небу руками; у него был такой вид, будто он только что выиграл в лотерею.
Это была хорошо продуманная система. Чтобы обозначить миллион, египетский писец мог не наносить на кость миллион зарубок, а просто нарисовать на папирусе фигурку коленопреклоненного человека. Такое умение легко записывать большие числа было одним из факторов, позволивших Египту превратиться в могущественную цивилизацию, способную успешно собирать налоги со своего населения и строить крупные города.
Но и в египетской системе было нечто весьма нерациональное. Если писец хотел записать число 9 999 999, он должен был использовать 63 символа. А если к этой сумме добавлялась еще одна единица, нужно было изобретать новый символ, обозначающий 10 000 000. Заметим теперь, что в нашей современной системе счисления для записи такого большого числа, как 9 999 999, мы используем всего семь символов, а при помощи всего десяти разных символов (0, 1, 2, … 9) можно записать сколь угодно большое число. Все дело в
Первой этот шорткат нашла цивилизация, соперничавшая с египетской, – вавилоняне. Интересно отметить, что в основе системы счисления их культуры лежали не степени десяти, как у египтян или в нашей нынешней системе. Они работали со степенями шестидесяти. У них были свои обозначения для всех чисел до 59, и только после этого, как они считали, требовалась перегруппировка. Числа от 1 до 59 они записывали с помощью всего двух символов: символа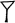 
, обозначавшего 1, и символа 
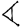, обозначавшего 10. Но это означало, что для записи числа 59 требовался набор из целых четырнадцати символов.
На первый взгляд такая система кажется далеко не рациональной. Но в выборе числа 60 скрывается шорткат совсем другого рода. Все дело в делимости этого числа. Число 60 можно представить в виде произведения стольких разных делителей – как 2 × 30, как 3 × 20, как 4 × 15, как 5 × 12 или как 6 × 10, – что у торговцев, которые брали на вооружение эту систему, было множество возможностей по-разному делить свои товары. Именно из-за высокой делимости числа 60 мы до сих пор используем его для отсчета времени. Час из шестидесяти минут и минута из шестидесяти секунд происходят из древнего Вавилона.
Однако по-настоящему революционным изобретением вавилонян была система представления чисел, больших 59. Можно было поступить как египтяне – то есть начать создавать новые символы. Но у вавилонян появилась другая идея: что значение символа может изменяться в зависимости от его положения относительно других символов. В нашей нынешней системе в числе 111 повторяется три раза один и тот же символ, и прелесть этого обозначения состоит в том, что, если читать это число справа налево, первый символ 1 обозначает единицу, второй – десяток, а третий – сотню. Каждый раз, когда мы добавляем слева еще один символ, его значение увеличивается в десять раз.