Быстроногий Ахилл хочет догнать неповоротливую черепаху. Она находится на сто шагов впереди него. Ахилл бегает в сто раз быстрее черепахи. Бег начался; когда Ахилл догонит черепаху? Неожиданный ответ: никогда! Ахилл пробежит эти сто шагов, но за это время черепаха уползет вперед еще на один шаг. Ахилл пробежит этот шаг, но черепаха уйдет вперед на сотую часть шага. Ахилл одолеет эту сотую, но черепаха оторвется от него еще на одну сотую сотой, и так далее, до бесконечности: разрыв между Ахиллом и черепахой будет все микроскопичнее, но не исчезнет никогда. Нелепость? Нелепость. А почему? Потому, что мы делили отрезки их пути до бесконечности.
Если, таким образом, самое беспорядочное на свете – это бесконечность, то что на свете самое упорядоченное, гармоничное, стройное? Единство. Если бы греки вышли против персов действительно «все как один», чтобы строй их был одним исполинским телом, – они победили бы врага немедленно. Единому вообще не нужна упорядоченность частей, потому что в нем нет частей – все однородно. Однородно не только в пространстве, но и во времени: единое не меняется, не крепнет и не слабеет, оно – вечно. Конечно, такого Единства никто никогда не видел, но всякий может его представить. Мы говорим «бог»; а что такое бог? Существо вечное и совершенное в каждой частице. Совершенное – значит «самое лучшее», а самое лучшее может быть только одно; вот это и есть Единство, однородное, вечное и божественное.
Парменид как бы заочно успокаивал плачущего Гераклита. Да, в окружающем нас мире все течет, рождается и умирает, но есть и другой мир, мир мысли, в котором все неизменно и вечно. В здешнем мире Пифагор давно умер, мы его не увидим и не услышим; но мы можем подумать о нем, и он предстает нашей мысли как живой, – это значит, что мы заглянули умственным взором в тот мир, где он вечно жив. Какой же из этих двух миров настоящий и какой ненастоящий? Нам хочется ответить: окружающий нас – настоящий, а мысленный – выдуманный. Парменид отвечал наоборот: мир мысли – настоящий, а мир наших ощущений – ненастоящий. Потому что в человеческом сознании мысль – хозяин, а чувства – ее рабы, которые лишь питают ее: одно – образами зрения, другое – образами слуха и так далее. А кому можно больше доверять, хозяину или рабам? Грек отвечал сразу и твердо: хозяину.
Не спешите смеяться над чудаком Парменидом, который в добавление к окружающему нас миру придумал несуществующий второй. Мы еще увидим, как пересочинит этот его второй мир философ Платон. И тем более не смейтесь над тем, как доказывал Зенон, что движения нет и Ахилл никогда не догонит черепаху. Показать, что это не так, очень легко: шаг, два – и готово. А вот доказать, почему это не так, очень трудно. И философы даже в наши дни порой спорят с Зеноном словно с современником.
«3 в квадрате будет 9», «3 в кубе будет 27». А вы задумывались, почему мы называем число, умноженное само на себя, квадратом, а умноженное само на себя и еще раз на себя – кубом? Потому что так представляли их греки. У них было, если можно так выразиться, зрительное мышление. Недаром в греческом языке «видеть» и «знать» были родственные слова (как в нашем – «видеть» и «ведать»). Оттого и был у греков такой сильный страх перед бесконечностью, что ее никак нельзя вообразить зрительно.
Нарисуйте в вашей тетрадке число 3 в виде трех точек подряд, как на кости домино. И подумайте: а как теперь удобнее всего нарисовать число 9? Очевидно – пририсовать над ним еще одно такое троеточие, а потом еще одно. Получится квадрат из 9 точек со стороной 3. Теперь возьмем три таких квадрата и положим их друг на друга. Получится куб из 27 точек со стороной 3. Вот так видели свои числа древние греки: как выложенные из камешков. Так что, кроме «квадратных» чисел, у них были и «продолговатые», а кроме «кубических» – и другие «объемные». Например, число 6 было продолговатым – как бы прямоугольником, у которого длина 3, а ширина 2. А число 30 – объемным: параллелепипедом, у которого длина 3, ширина 2, а высота 5.
(Почему «2 в квадрате – 4» – теперь понятно; но почему «2 – квадратный корень из 4»? Слово «корень» ввели в математику уже не греки, а арабы. Они предпочитали представлять мир не геометрическим, как греки, а органическим; и в этом мире из числа 2, как растение из корня, вырастает число 4, а потом 8, а потом 16 и все остальные степени.)
При греческом зрительном воображении принято было перестраивать числа из фигуры в фигуру: например, представлять число 12 то как длинный узкий прямоугольник 6×2, то как короткий и широкий 3х4. Поэтому греки обращали большое внимание на набор делителей числа. Например, если число равнялось сумме собственных делителей, оно называлось «совершенным». Греки знали четыре таких числа – 6, 28, 496 и 8128. (Если хотите, убедитесь: 6=1+2+3
Неудобства начинались при обращении с дробями: ведь точку не раздробишь на части. Поэтому греки предпочитали иметь дело не с дробями, а с отношениями: говорили не «одна седьмая часть единицы», а «одна единица от семи». Отношения и пропорции они сортировали с большой любовью. Мы говорим: «Число 20 кратно числу 5», то есть делится на него. А грек мог вдобавок сказать: «Число 20 кратночастно числу 16», то есть делится на разность между ними. Вы знаете: число 4 – это среднее арифметическое чисел 2 и 6, то есть сумма их, деленная пополам. Некоторые, может быть, знают: число 4 – это среднее геометрическое чисел 2 и 8, то есть квадратный корень из их произведения. А грек вдобавок знал: число 4 – это «среднее гармоническое» чисел 3 и 6, то есть их удвоенное произведение, деленное на их сумму.
Когда вы начинали учить алгебру, то заучивали такие формулы, как:
(a + b)2 = a2 + 2ab + b2;
(a – b)2 = a2 – 2ab + b2;
a2 – b2 = (a + b) (a – b).
Вы помните, как они выводились? Это было довольно громоздко. А грек со своей привычкой к наглядности доказывал их не вычислением, а чертежом: чертил отрезок А, отрезок В, строил на них квадраты и показывал: «Вот!» Посмотрите и убедитесь.
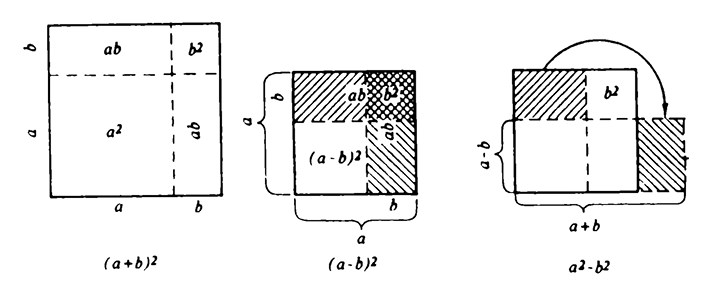
Такие геометрические доказательства выручали греков в их страхе перед бесконечностью. Вы смогли бы, например, извлечь точный корень из числа 2? Нет, не смогли бы: получили бы бесконечную дробь. А греческий математик поступал просто: чертил отрезок длиной в данное число, строил вокруг квадрат, в котором он был бы диагональю, показывал на сторону этого квадрата и говорил: «Вот!»
В современной математике такие величины, никогда не вычисляемые до конца, называются иррациональными. Греки называли их «невыразимые». «Невыразимым» было отношение диагонали и стороны в квадрате – 1,41421…; «невыразимым» было и отношение длины окружности к диаметру в круге, знаменитое число «пи» – 3,14159… («пи» – это первая буква греческого слова «периферия», окружность). Это число изобразить было труднее, и греческие математики в своей борьбе с бесконечностью век за веком ломали голову над «квадратурой круга»: как по данному диаметру круга с помощью только циркуля и линейки построить квадрат, равновеликий этому кругу?
Можно задать вопрос: а почему, собственно, с помощью только циркуля и линейки? Не попробовать ли изобрести новый прибор, посложнее, который позволил бы решить эту задачу? Но грек нам гордо ответил бы: «Возиться с приборами – это дело раба, привычного к ручному труду, а свободному человеку приличествует полагаться лишь на силу ума».
Вот как, оказывается, рабовладельческий образ мысли проявляется даже в такой отвлеченной науке, как математика.
Гераклита и Парменида решил помирить сицилиец Эмпедокл. Он сказал: «Ни война, ни мир на земле не вечны. Так и во вселенной. Они сменяют друг друга, как времена года. Мир шарообразен, но этот шар неоднороден. В нем смешаны четыре стихии: земля, вода, воздух, огонь. А над ними властвуют две силы: Любовь и Вражда. Наступает пора мира – и в центре мирового шара царствует Любовь, она сливает вокруг себя четыре стихии в то самое Единство, о котором мечтал Парменид, а Вражда отступает и лишь снаружи облегает мировой шар. Наступает новая пора – и Вражда со всех сторон начинает проникать в мир, вытесняя из него Любовь, а на пути своем она разобщает четыре стихии, и они встают войной друг на друга. Наконец Вражда восседает в центре мира, вокруг нее кипит гераклитовская война четырех стихий, а Любовь оттеснена наружу и ждет своего часа. А потом все повторяется в обратном порядке. Если это на что-нибудь похоже, то больше всего – на гражданский мир и гражданскую войну в городе, где есть несколько политических партий. Сейчас мир на полпути: то ли от Вражды к Любви, то ли наоборот».
Как Фемистоклу не давали спать лавры Мильтиада, так Эмпедоклу – лавры Пифагора. Он тоже хотел быть пророком и чудотворцем. Когда ему предложили царскую власть, он отверг ее: «Лучшее из растений – лавр, из животных – лев, из людей – мудрец, а вовсе не царь». Держался он еще величавее, чем царь, носил пурпурный плащ, золотую повязку на голове и медные сандалии. Учение свое он изложил стихами и читал эти стихи в Олимпии. А когда в Олимпии его колесница одержала победу на играх, он принес в жертву быка из медового теста и пряностей, потому что пифагорейский закон запрещал убивать животных.