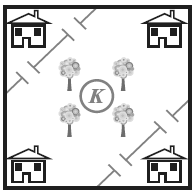
На рисунке изображена деревня, в которой находятся четыре дома, четыре дерева, две изгороди с четырьмя калитками. В центре деревни расположен колодец с питьевой водой. Необходимо разделить территорию деревни на четыре равных участка таким образом, чтобы каждому домовладельцу досталось по одному дереву, по куску изгороди равной длины и по свободному проходу к колодцу, который не пересекал бы участок соседа.

Проведите три прямые линии таким образом, чтобы отделить собачек от косточек.
При помощи четырех костей домино можно изобразить умножение трехзначного числа на однозначное. На рисунке показан пример 551×4=2204. И 28 костей домино можно сложить 7 «умножений», подобных показанному на рисунке. Шесть «умножений» вы построите без особого труда. А вот над седьмым придется подумать – все же это возможно.

У Джона был небольшой парк из десяти деревьев, которые располагались в два ряда по пять деревьев. Ему показалась такая рассадка очень скучной и Джон решил пересадить эти деревья таким образом, чтобы после пересадки они образовали между собой пять рядов, по четыре дерева в каждом ряду.
Как ему это удалось?

Разместите восемь бабочек на линиях рисунка так, чтобы на каждой окружности и на каждой из четырех прямых линий было по две бабочки.
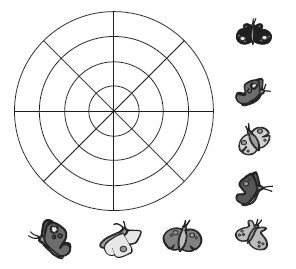
Эту задачу придумал английский математик Чарлз Доджсон, он же Льюис Кэрролл, автор известной детской книги “Алиса в стране чудес”.
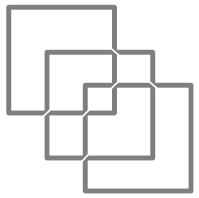
Вам необходимо нарисовать фигуру, указанную на рисунке не отрывая карандаша от бумаги и не проводя дважды одну и ту же линию. Задача усложняется тем, что линии не должны нигде пересекаться между собой (допускается только угловое касание линий).
В этом ребусе зашифровано название книги братьев – фантастов.

Оригинальный орнамент, изображенный на рисунке, состоит из 16 маленьких треугольников. Некоторые группы из четырех соседних маленьких треугольников образуют большие треугольники. В орнаменте прорисовано шесть больших треугольников, «сплетенных» между собой.
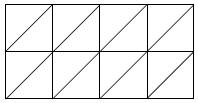
Вам необходимо вписать в каждый маленький треугольник орнамента одно из целых чисел от 1 до 16 (не повторяя их) таким образом, чтобы сумма чисел в любом из шести больших треугольников равнялась 34.
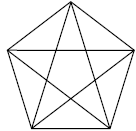
Данная геометрическая фигура включает в себя множество треугольников.
Проверьте свою геометрическую смекалку и сосчитайте сколько их.
На главной площади провинциального городка шла подготовка к празднику 9 Мая. Ученикам местной школы было поручено украсить площадь гирляндами, шарами и флагами. Флагов было лишь 12. Сначала школьники расставили их по 4 штуки с каждой стороны как показано на рисунке.
Потом сообразили, что эти же 12 флагов они могут расставить по 5 и даже по 6 с каждой стороны.
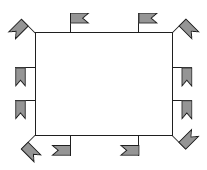
Покажите на схеме, как ученики расставили 12 флагов по 5 с каждой из четырех сторон и как они могли бы их расставить по 6.
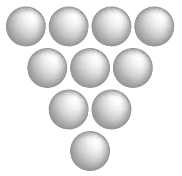
Переложите всего три шарика, так чтобы получился точно такой же треугольник, но перевернутый вверх ногами.
В столбике слева 14 слов. В каждом слове, начиная со второго, число букв на одну больше, чем в предыдущем. В последнем слове «самообразование» – 15 букв.
Из всех этих четырнадцати слов выберите четыре слова так, чтобы были справедливыми следующие два равенства:
a2=bd, ad=b2c