«Событие А называется частным случаем события B, если при наступлении А наступает и B.
То, что А является частным случаем В, записываем
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
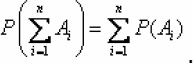
Если случайные события образуют полную группу несовместных событий, то имеет место равенство:
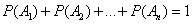
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле:
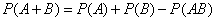
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно.
Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
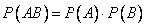
Перед дверью аудитории толпились студенты. Экзамен начался двадцать пять минут назад, профессор запустил первую пятерку, и она должна была выйти не раньше, чем часа через полтора.
Кирилл стоял в одиночестве неподалеку, прислонившись к стене. Настроение было паршивым. Вчера он планировал отстреляться прямо с утра, но чуть-чуть проспал – и поэтому сейчас должен бестолково ждать своей очереди, теряя время.
– Ну, и? – в связи с изменениями в планах, Кирилл пытался оптимально подкорректировать расписание дня. – Что лучше: ждать следующей пятерки или вернуться в общагу и пойти на экзамен уже ближе к вечеру – часикам к трем? К тому времени как раз бо́льшая половина группы уже сдаст. Наверное, все же возвращаться в общагу ни к чему – вдруг профессор решит ускориться! Тогда пойду в буфет, а потом – в «сачок».
Кирилл забросил рюкзак с учебниками и конспектами за спину и двинулся вдоль по коридору. Повернул за угол и нос к носу столкнулся с Машей. Вид у девушки был веселый и расслабленный. И, конечно, она была очень красива. И очень стильно одета – как всегда. И, конечно, рядом с ней подобострастно труси́ли несколько парней и девушек из ее группы.
– О, привет! – завидев Кирилла, Маша остановилась. Вместе с ней, как по команде, встала и свита – по лицам дам и джентльменов блуждали недовольные тени-выражения. – Ты куда пропал, почему не звонишь?